Решение задач линейного программирования симплекс-методом — это решение задач линейного программирования путём нахождения исходного допустимого плана с последующим улучшением плана, вплоть до достижения экстремального значения целевой функции.
Введение
Симплекс метод - это метод поочерёдного перемещения от одного основного решения системы ограничений задачи линейного программирования к другому основному решению до того момента, пока целевая функция не достигнет требуемого экстремального значения, то есть, своих максимальных или минимальных значений.
Симплекс-метод считается универсальным методом, при помощи которого может быть решена любая задача линейного программирования, при этом, следует отметить, что графический метод может быть использован только для системы ограничений с двумя переменными. Симплекс метод разработал американский математик Р. Данциг в 1947-ом году, с той поры многие специалисты при помощи этого метода решают задачи линейного программирования, в которых присутствуют многие тысячи переменных и ограничений.
Решение задач линейного программирования симплекс-методом
Любое неотрицательное решение системы ограничений именуется допустимым решением. Предположим есть система m ограничений с n переменными (m меньше n). Допустимым базисным решением считается решение, которое содержит m неотрицательных основных, то есть базисных, переменных и (n – m) неосновных, то есть небазисных или свободных переменных. Неосновные переменные в базисном решении равняются нулю, основные же переменные обычно отличаются от нуля, что означает, что они положительные числа.
Любые m переменных системы m линейных уравнений с n переменными являются основными в случае, когда определитель из коэффициентов при них отличается от нуля. В таком случае остальные n - m переменных могут считаться неосновными или свободными.
Симплекс метод может быть представлен следующим алгоритмом:
- Сначала следует представить задачу линейного программирования в канонической форме. Для этого необходимо перенести все свободные члены в правые части (в случае, когда среди данных свободных членов имеются также отрицательные, то такие уравнения или неравенства следует умножить на минус единицу) и во все ограничения добавить дополнительные переменные, имеющие знак плюс, если в исходном неравенстве знак «меньше или равно», и имеющие знак минус, если в исходном неравенстве «больше или равно».
- Если в сформированной системе получилось m уравнений, то m переменных следует считать основными. Далее нужно отобразить основные переменные через неосновные и определить необходимое базисное решение. Если вычисленное базисное решение будет допустимое, то следует перейти к допустимому базисному решению.
- Далее необходимо найти выражение функции цели через неосновные переменные допустимого базисного решения. В случае, когда ищется экстремум линейной формы и в его выражении не присутствуют неосновные переменные с отрицательными (положительными) коэффициентами, то условие оптимальности считается выполненным и найденное базисное решение может считаться оптимальным, то есть, процесс решения завершён. Если при определении экстремума линейной формы в её выражении присутствует одна или больше неосновных переменных с отрицательными (положительными) коэффициентами, то следует осуществить переход к новому базисному решению.
- Из совокупности неосновных переменных, которые входят в линейную форму с отрицательными (положительными) коэффициентами, следует выбрать ту, которой будет соответствовать самый большой (по модулю) коэффициент, и перевести её в основные. Далее необходимо перейти ко второму этапу.
При реализации алгоритма симплекс-метода, необходима соблюдать следующие важные условия:
- В случае, когда допустимое базисное решение представляет собой оптимум линейной формы, то есть исполнен критерий оптимальности, а в выражении линейной формы, представленной неосновными переменными, не присутствует хотя бы одна из них, то, следовательно, найденное оптимальное решение не является единственным.
- В случае, когда в выражении линейной формы присутствует неосновная переменная с отрицательным коэффициентом в варианте нахождения её максимума (с положительным коэффициентом в случае нахождения её минимума), а в каждое уравнение системы ограничений данного этапа эта переменная включена также с отрицательным коэффициентом или отсутствует, то линейная форма ничем не ограничивается при существующей ограничительной системе. В таком варианте экстремум линейной формы будет равняться плюс или минус бесконечности.
Следует отметить, что в сети Интернет имеются сайты с онлайн калькуляторами, предназначенными для решения задач линейного программирования симплекс-методом.
Рассмотрим стандартный пример, когда система ограничений рассматривается как совместимая и присутствует единственное конечное оптимальное решение.
Задачи линейного программирования могут решаться также симплекс-методом, но с использованием специальных симплексных таблиц. Построение симплексных таблиц позволяет найти решение задачи линейного программирования значительно проще, чем при использовании алгебраических преобразований. Симплексные таблицы обладают достаточно наглядным отображением. Известны различные наборы правил по работе с симплексными таблицами. В том числе правило, которое наиболее часто рассматривается как правило ведущих столбцов и ведущих строк.
Необходимо определить максимум следующей функции:
$F=x_1 + 2x_2$
При наличии следующих ограничений:
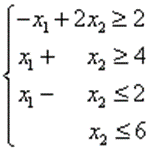
Рисунок 1. Ограничения. Автор24 — интернет-биржа студенческих работ
$x_1≥0, x_2 ≤ 0$
Сначала необходимо добавить некоторые переменные x3, x4, x5, x6, которые должны быть неотрицательными, и свести эту систему неравенств к эквивалентной ей системе уравнений:
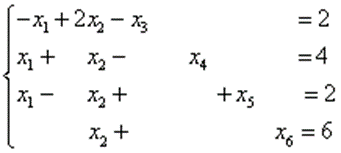
Рисунок 2. Система уравнений. Автор24 — интернет-биржа студенческих работ
$ X_j ≥0 (j=1, 2, …6)$
Из коэффициентов при переменных (неизвестных) может быть построена симплексная таблица. В последнюю строку таблицы должна быть записана целевая функция. Эта строка называется индексной строкой.












