Целые числа являются самыми простыми числовыми данными, с которыми работает компьютер. Целые числа хранятся в двух возможных видах: беззнаковом (для положительных целых чисел) и со знаком (для отрицательных чисел). Целые числа в компьютере хранятся в формате с фиксированной запятой.
Беззнаковые целые числа
Для беззнакового представления все разряды ячейки отводятся под представление самого числа. Поэтому, если известно, что число положительное, то выгоднее рассматривать его как беззнаковое.
Положительные целые числа занимают в памяти компьютера $1$ или $2$ байта.
В $1$-байтовом формате целые числа принимают значения от $0$ до $255$.
В $2$-байтовом формате от $0$ до $65535$.
Число $30_{10}=0001 \ 1110_2$ в $1$-байтовом формате:
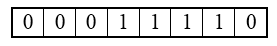
Рисунок 1.
Число $30_{10}=0001 \ 1110_2$ в 2-байтовом формате:

Рисунок 2.
Алгоритм представления в компьютере беззнаковых целых чисел
-
Беззнаковое целое положительное число перевести в двоичную систему счисления.
-
Записать число в $8$ разрядах так, чтобы младший разряд числа соответствовал младшему разряду ячейки.
-
Дополнить число, если необходимо, слева нулями до нужного числа разрядов ($8$-ми, $16$-ти, $32$-х).
Получить 8-разрядное представление числа $30$.
-
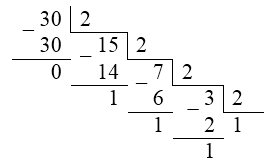
Рисунок 3. -
$30_{10}=11110_2.$
-
Дополним до $8$-ми разрядов:
Целые числа со знаком
Целые числа со знаком (отрицательные) занимают в памяти компьютера $1$, $2$ или $4$ байта, при этом самый старший (знаковый) разряд содержит информацию о знаке числа.
Если число положительное, то в знаковом разряде помещается $«0»$, если число отрицательное -- $«1»$.
Целые числа со знаком в разных форматах принимают соответствующие значения:
-
в $1$-байтовом формате -- от $-128$ до $127$;
-
в $2$-байтовом формате -- от $-32768$ до $32767$;
-
в $4$-байтовом формате -- от $-2147483648$ до $2147483647$.
Для хранения целых чисел со знаком отводится $1$ разряд для знака, а остальные -- для цифр модуля числа.
Например, для хранения числа в $1$-байтовом формате ($8$ бит) $1$ разряд отводится для знака числа, остальные $7$ разрядов -- для модуля числа.
Для хранения целых чисел со знаком применяется $3$ формы кода:
-
прямой;
-
обратный;
-
дополнительный.
Особенно широко используется обратный и дополнительный код, которые позволяют существенно облегчить элементарные операции: сложение, вычитание, умножение и деление.
Положительные числа в прямом, обратном и дополнительном кодах изображают двоичными кодами с цифрой $0$ в знаковом разряде.
У положительных чисел все коды одинаковы, т.е. прямой, обратный и дополнительный коды равны между собой.
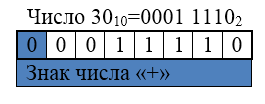
Рисунок 4.
Отрицательные числа в прямом, обратном и дополнительном кодах изображаются по-разному.
-
Прямой код числа -- это его модуль, переведенный в двоичную систему с измененным старшим битом, в зависимости от знака.
В знаковом разряде помещается цифра $1$, а в разрядах цифровой части числа -- двоичный код модуля числа.
Числа в компьютере хранятся целыми байтами; $1$, $2$, $4$ или $8$. От количества памяти зависит количество разрядов данного числа. В $1$ байте их $8$, в $2$ - $16$ и т.д. Поэтому представляемые числа нужно дополнять нулями до необходимого количества.
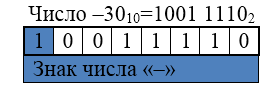
Рисунок 5.Если числа будут занимать в памяти $2$ байта, то знаковым все равно будет самый старший, то есть: $-30_{10}=1001 \ 1110_2= 1000 \ 0000 \ 0001 \ 1110_2$
-
Обратный код. Для операций с отрицательными числами обычно не используется прямой код, поэтому для облегчения алгоритмов выполнения арифметических операций был создан обратный код.
Для получения обратного кода выполняется инвертирование всех цифр двоичного кода модуля числа: $0$ заменяется на $1$, а $1$ - на $0$. Знак разряда остается без изменений.
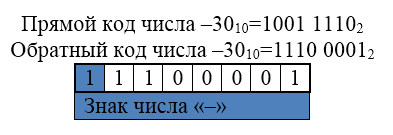
Рисунок 6. -
Дополнительный код
Для получения дополнительного кода числа к обратному коду добавляется единица к его младшему разряду.
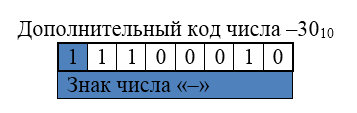
Рисунок 7.
Алгоритм получения дополнительного кода отрицательного числа
-
Модуль отрицательного числа представить прямым кодом.
-
Значение всех бит инвертировать: все $0$ заменить на $1$, а $1$ на $0$ (кроме значения знакового разряда).
-
К младшему разряду полученного обратного кода прибавить единицу.
Получим $8$-разрядный дополнительный код числа $-30$:
$00011110 - \ число \mid -30\mid =30$ в прямом коде
$11100001 - \ число \ -30$ в обратном коде
$11100010 - \ число \ -30$ в дополнительном коде
Целые отрицательные числа при вводе в компьютер преобразуются в обратный или дополнительный двоичный код и в таком виде хранятся и принимают участие в операциях. При выводе их из компьютера происходит обратное преобразование в отрицательные десятичные числа.











