К простым структурам информации относятся:
- множества;
- линейный список;
- таблицы.
Самой простейшей структурой является множество, то есть, некоторый набор элементов. Чтобы определить множество, необходимо перечислить все его элементы или описать и определить характерный признак элементов множества.
Множество может состоять из конечного числа элементов (например, алфавит), бесконечного числа элементов (например, множество чисел) или вообще быть пустым (например, множество попугаев, живущих на Северном полюсе). В документах конечное множество часто оформляют в виде маркированного списка. В таком списке порядок элементов не важен, от перестановки элементов само множество не меняется.
Если множество состоит из конечного числа элементов и его элементы должны быть расположены в строго определенном порядке, мы получаем линейный список. Список обычно упорядочен (отсортирован) по какому‐то правилу, например, по алфавиту, по важности, по последовательности действий и т.д.
Переставить местами элементы такого списка нельзя (это будет уже другой список). Линейный список может быть представлен в виде цепочки связанных элементов:
Рисунок 1.
Список можно задать перечислением элементов, с первого до последнего:
(надеть носки, надеть ботинки, выйти из дома)
Поменяв местами "надеть ботинки" и "надеть носки", получим новый список: "надеть ботинки, надеть носки, выйти из дома".
В теории информатики линейный список определяется как конечная последовательность однотипных элементов (узлов), возможно, с повторениями. Список характеризуется длиной или количеством элементов, причем длина списка в процессе работы программы может изменяться. В список могут быть добавлены или удалены данные.
На практике программирования линейные списки реализованы при помощи массивов (array) и связных списков (динамических массииивов). Термин «список» часто используется также как синоним понятия «связный список».
Конструктор операций со списками представлен следующим образом:
- проверка списка на пустоту (NULL);
- добавлениеобъектов в список;
- определение голвного (первого) элемента списка;
- определение функционала доступа к списку (последовательный или по индексу).
Списки могут быть типизированными или нетипизированными. Если список типизирован, то все его элементы имеют заданный тип. Списки, реализованные при помощи массивов данных, являются типизированными.
В программировании списки называют стеками и очередями.
Список может быть сортированным или несортированным.
В зависимости от реализации может быть возможен произвольный доступ к элементам списка. Например, есть возможность обработать любой элемент массива по его индексу (порядковому номеру).
Еще одна простая структура представления информации – таблица.
Преимущество структурирования информации в виде таблиц заключается в том, что таблицы легко обрабатывать. К недостатку можно отнести тот факт, что не всю информацию можно представить в виде таблицы (например, архив судебных дел).
При структурировании информации с помощью таблиц устанавливается зависимость между несколькими элементами. Например, в следующей таблице элементы в каждой строке связаны между собой – это свойства некоторого объекта (человека):
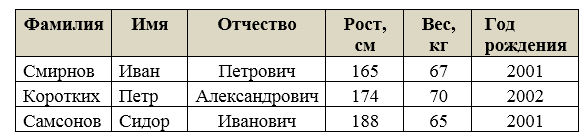
Рисунок 2.
Табличный метод используется при создании баз данных. Строка таблицы, содержащая информацию об одном объекте, называется записью, а столбец (название свойства) – полем. Так характеризуются данные реляционной базы данных.
Возможен и другой вариант таблицы, когда роли строк и столбцов меняются. В первом столбце записываются названия свойств, а данные в каждом из следующих столбцов описывают свойства какого‐то объекта. Например, вот таблица с характеристиками разных продуктов:
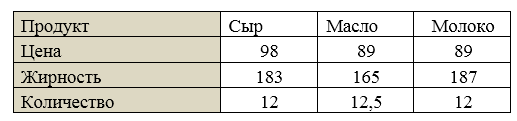
Рисунок 3.
В математике и программировании таблицы обычно называют матрицами.
Матрица — математический объект, записываемый в виде прямоугольной таблицы элементов (например, целых, действительных или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задает размер матрицы. Матрицы бывают прямоугольные, где количество строк не равно количеству столбцов и квадратные, где количество строк равно количеству столбцов.
Применение матричной формы широко используется при записи систем линейных алгебраических или дифференциальных уравнений. В результате решение системы линейных уравнений сводится к выполнению операций над матрицами.
Для матрицы определены следующие алгебраические операции:
- сложение матриц, имеющих один и тот же размер;
- умножение матриц подходящего размера;
- умножение вектора на матрицу (вектор является частным случаем матрицы);
- умножение матрицы на элемент основного кольца или поля (то есть скаляр).
Эсли система алгебраических уравнений имеет следующий вид:
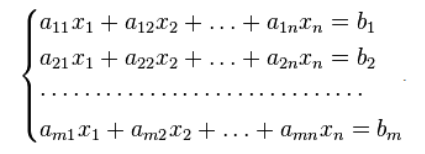
Рисунок 4. Система уравнений
то элементы системы алгебраических уравнений в матричном виде будут иметь вид, представленный на рисунке 5 и математически записывается $Ax=B.$
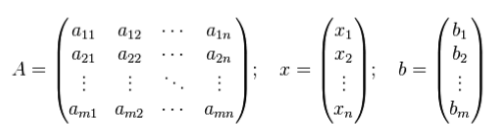вектора">
Рисунок 5. Матрица и два вектора
