Логические выражения называются равносильными, если их итоговые значения совпадают при любых значениях входящих в них логических переменных.
В алгебре логики есть законы, которые позволяют выполнять равносильные преобразования логических выражений. Примеры соотношений, которые отражают эти законы.
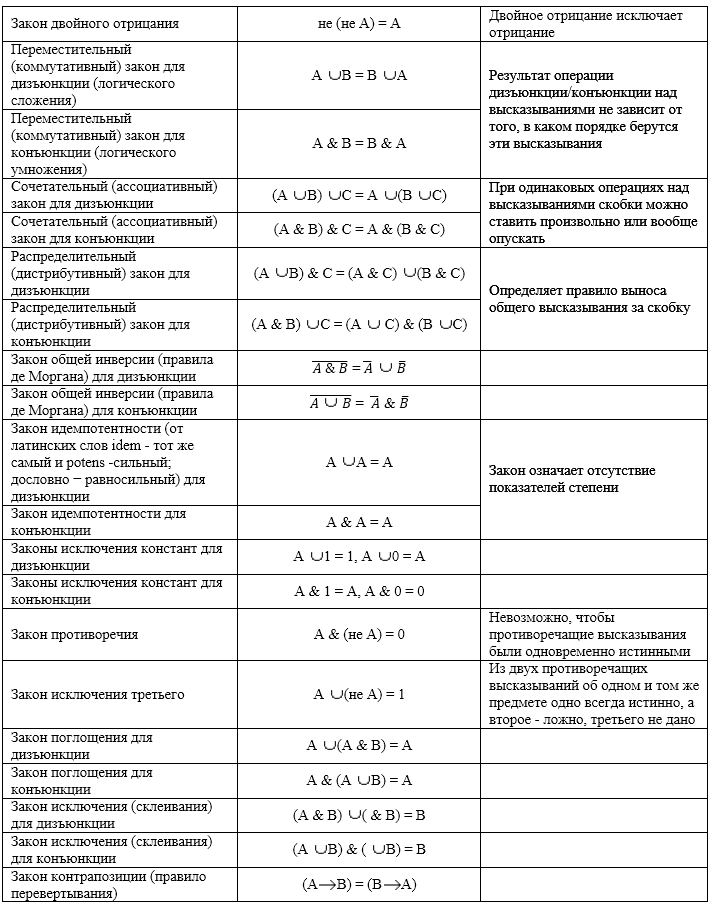
Рисунок 1.
Справедливость приведенных законов можно доказать при помощи таблиц истинности: выписать все наборы переменных $A$ и $B$, вычислить на этих наборах значения левой и правой частей доказываемого выражения, сравнить столбцы результатов и убедиться, что они совпали.
Доказать, используя таблицы истинности, что логические выражения равносильны
$A \to B = \bar{A} \cup B$
Составим таблицы истинности для этих выражений

Рисунок 2.
Результирующие столбцы левого и правого выражений совпадают, значит, эти выражения равносильны.
Доказать, при помощи таблиц истинности, что операция эквивалентности равносильна выражению
$А \leftrightarrow В$ = ($А \cup \overline{В}$) & ($\overline{А} \cup В$)

Рисунок 3.
Результирующие столбцы левого и правого выражений совпадают, значит, эти выражения равносильны.
Упростить логическое выражение:

Рисунок 4.
Чтобы проверить, верно ли выполнено задание, надо проверить, являются ли исходное и полученное выражения равносильными, составим таблицы истинности для этих выражений:
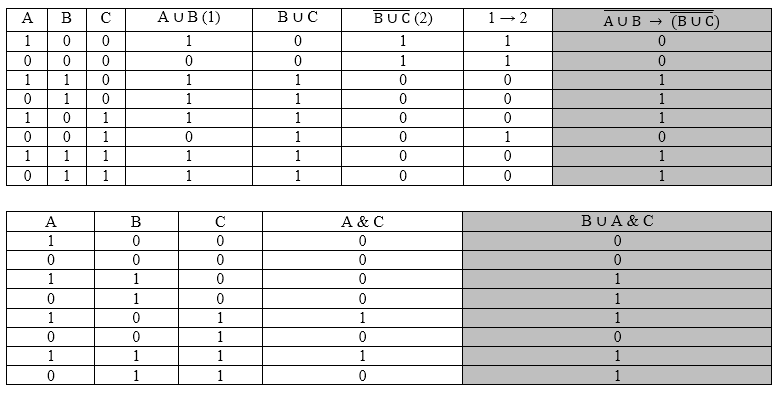
Рисунок 5.
Результирующие столбцы исходного и полученного выражений совпадают, значит, эти выражения равносильны, и упрощение выполнено правильно.












