Алгебра высказываний

Используя определение высказывания, определим, можно ли считать высказываниями следующие предложения:

1. Сейчас идет снег.
2. Вчера крокодилы улетели на юг.
3. Прекрасно!
4. Сколько времени необходимо для приготовления блюда?
5. В городе $N$ живут более $5$ миллионов человек.
6. Посмотрите на картину.
7. У прямоугольника $10$ сторон, и все они разные.
8. Биология – интересный предмет.

В приведенных примерах высказываниями являются предложения 1, 2 и 7, остальные примеры не являются высказываниями. Утверждения 3 и 4 – это восклицательное и вопросительное предложения, а не повествовательные предложения, как определяется высказывание. Предложение 5 станет высказыванием только в том случае, если $«N»$ заменить на конкретное название города. Пример 6 – побудительное предложение, призыв к действию, а не утверждение. Утверждение примера 8 кто‐то может считать истинным, а кто‐то ложным (нет однозначности). Пример 8 можно более строго сформулировать в виде «По мнению $N$, биология – интересный предмет». Для того, чтобы утверждение примера 8 стало высказыванием, нужно заменить $«N»$ на конкретное имя человека.

В формальной логике высказывание может быть ложно или истинно, третьего варианта исключено. Обозначим истинное значение за единицу, а ложное за нуль, то получим, что формальная логика представляет собой правила выполнения операций с двоичными кодами (нулями и единицами). Тогда обработка информации сводится к выполнению логических операций над нулями и единицами. Важный шаг в этом направлении сделал английский математик Джордж Буль. Дж.Буль предложил применять для исследования логических высказываний на их истинность или ложность математический механизм. Позже этот раздел математики стали называть алгеброй логики или булевой алгеброй.

Рисунок 1. Дж. Буль (1815‐1864)

Алгебра логики определяет правила выполнения операций с логическими величинами, которые могут быть равны только $0$ или $1$, то есть с двоичными данными.

Высказывания бывают простые и сложные (составные). Простые высказывания невозможно разделить на более мелкие высказывания, например: «Утро теплое» или «Форточка закрыта». Сложные (составные) высказывания строятся из простых высказываний с помощью логических связок или операций: «И», «ИЛИ», «НЕ», «если…, то», «тогда и только тогда».

В булевой алгебре высказывания обычно обозначаются латинскими буквами, благодаря чему происходит уход от конкретного содержания высказывания, и при помощи математического механизма булевой алгебры определяется истинность или ложность высказываний. Например, можно обозначить буквой $A$ высказывание «Утро теплое», а буквой $B$ – высказывание «Форточка закрыта» и построить сложные высказывания:

• Не $A$: «Утро не теплое» или «Неверно, что утро теплое».

• Не $B$: «Форточка открыта» или «Неверно, что форточка закрыта».

  Отрицание всегда ставится к действию.

• $A$ и $B$:«Утро теплое и форточка закрыта».

• $A$ или $B$: «Утро теплое или форточка закрыта».

• если $A$, то $B$: «Если утро теплое то форточка закрыта».

• тогда и только тогда: «Утро теплое тогда и только тогда, когда форточка закрыта».

Операции «НЕ», «И» и «ИЛИ» используются чаще других. С помощью этих операций можно описать любое действие, поэтому они называются основными или базовыми операциями.

Операция «НЕ» часто называется инверсией или отрицанием. В булевой алгебре всего два символа, $0$ и $1$, поэтому логические отрицание – это переход от одного значения к другому. Если высказывание В истинно, то тогда «не $В$» ложно, и наоборот.

Операция «НЕ» обозначается несколькими способами. Выражение «не $А$» в алгебре логики записывается как $\bar{A}$ или $¬A$, в языках программирования в Бейсике и Паскале – как not A, в языке Си – как !A. Это унарная операция.

Таблица истинности для отрицания:

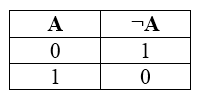
Рисунок 2.

Операция «И» - конъюнкция (в отличие от «НЕ») выполняется с двумя логическими значениями. Это бинарная операция. Результат этой операции в алгебре логики записывают как $A$ $B$, $A ∧ B$ или $A$ & $B$. В языках программирования используют обозначения «$A$ and $B$» (Бейсик и Паскаль) или «$A$ && $B$» (Си).

В таблице истинности будет два столбца с исходными значениями.

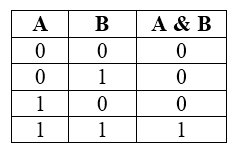
Рисунок 3.

Операцию «ИЛИ» часто называют логическим сложением, и она похожа на обычное математическое сложение кроме единственных значений в последней строке таблицы истинности для набора $1$ $1$: в математике $1+1$ равно $2$, а в алгебре логики – $1$, $2$ нет в символике алгебры логики. Операция «ИЛИ» – дизъюнкция (в переводе с латинского – разделение).

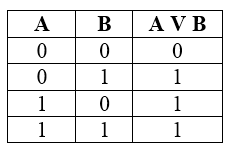
Рисунок 4.

Возможны и другие обозначения $A \cdot V \cdot B$ и $A+B$.

В алгебре логики доказано, что операций «НЕ», «И» и «ИЛИ» достаточно для того, чтобы записать с их помощью любую другую логическую операцию, которую только можно придумать. Операций «НЕ», «И» и «ИЛИ» являются базисом или базовыми операциями.

Мы часто используем логическую связку «если…, то», например: «Если пойдет дождь, то открою зонт» или «Если все стороны треугольника равны, то этот треугольник равносторонний». В алгебре логики эта связка называется импликацией (следованием) и обозначается стрелкой: $A → B$ («если $A$, то $B$», «из $A$ следует $B$»). Таблица истинности выглядит следующим образом:

Рисунок 5.

Значение импликации всегда равно единице, кроме одного набора $1$ $0$.

Импликацию можно заменить на выражение, использующее только базовые операции: $A → B = ¬A+ B$.

Эквивалентность (также равносильность, эквиваленция) – это логическая операция, соответствующая связке «тогда и только тогда» или «необходимо и достаточно».

Пример использования эквиваленции: «Треугольник равносторонний тогда и только тогда, когда все стороны имеют одинаковую длину». Высказывание $A↔B$ истинно только в том случае, когда $A = B$, т.е. на равных наборах значений принимает значение $1$, а на неравных наборах значений принимает значение $0$ (см. таблицу истинности).

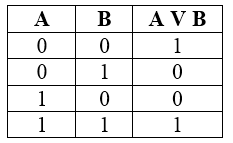
Рисунок 6.