Логика - очень древняя наука. В античные времена, в древней Греции, Древней Индии, Древнем Риме, развивалась формальная логика, позволяющая делать заключения о правильности какого-либо суждения не по его фактическому содержанию, а по форме его построения, были выстроены законы: исключения третьего, закон непротиворечивости и закон отрицания, на которых основывалось ораторское искусство. Применение логических приемов рассуждения позволяло ораторам более убедительно доносить до аудитории их точку зрения, склонять людей на свою сторону.
Мыслить логично – значит мыслить точно и последовательно, не допускать противоречий в своих рассуждеиях, уметь выявлять логические ошибки.
Основателем Логики считается величайший древнегреческий философ Аристотель, который первым систематизировал формы и правила мышления, обстоятельно исследовал категории «понятие» и «суждение», подробно разработал теорию умозаключений и доказательств, описал ряд логических операций, сформулировал основные законы мышления.

Рисунок 1. АРИСТОТЕЛЬ (Aristoteles) Стагирский 384 – 322 до н. э.
Логика изучает следующие формы: суждение, понятие, умозаключение и доказательство.
Суждение является формой мышления, утверждающей или отрицающей что-либо о существовании предметов, о связях между ними и их свойствами, а также об отношениях между предметами. Суждение включает в себя следующие элементы: субъект, предикат, связка и квантор. Все суждения бывают истиными и ложными. Суждение является истинным в том случае, когда наличие признаков, свойств и отношений предметов, утверждаемых/отрицаемых в суждении, соответствует действительности. Например: «Все ласточки – птицы», «$9$ больше $2$-х» и т. д. Если утверждение, содержащееся в суждении, не соответствует действительности, мы имеем дело с ложным суждением: «Солнце вращается вокруг Земли», «Килограмм железа тяжелее, чем килограмм ваты» и др. Правильные суждения составляют основу правильных умозаключений.
Понятие - это форма мышления, которая отражает наиболее существенные свойства самого предмета. В структуре каждого понятия различают две стороны: объём и содержание. Содержание понятия составляет совокупность существенных признаков предмета. Чтобы раскрыть содержание понятия выделяют необходимые и достаточные признаки для того, чтобы выделить данный предмет из других предметов. Объем понятия определяется множеством всех предметов, на которые оно распространяется, и может быть представлено в совокупности множеств объектов, состоящих из элементов множества. Между объемами понятий могут быть различные виды отношений:
-
равнозначность, когда объемы понятий полностью совпадают;
-
пересечение, когда объемы понятий частично совпадают;
-
подчинения, когда объем одного понятия полностью входит в объем другого и т.д.
Примеры сравнения отношений между понятиями:
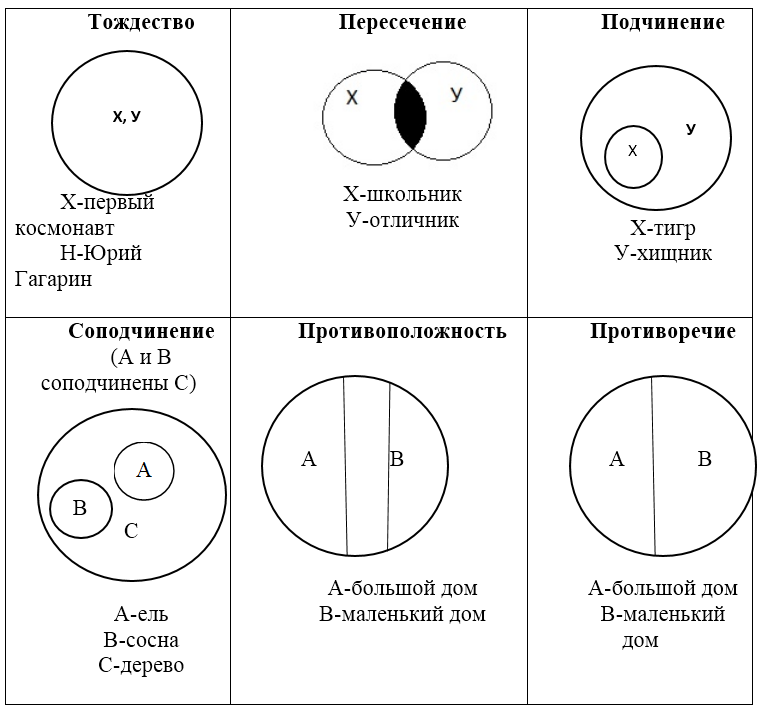
Рисунок 2.
Формальная логика развивалась и обогащалась новыми законами и правилами, но при этом вплоть до $XIX$ века она оставалась обобщением конкретных содержательных данных и её законы сохраняли форму высказываний на разговорном языке.
В 1847 году английский математик Джордж Буль, преподаватель провинциального университета в маленьком городке Корке на юге Англии разработал алгебру логики. Идея была очень простой, так как каждая переменная может принимать только два значения: истинно или ложно, - то в соответствие этим значениям ставится или $0$. Логическая $1$ означает, что какое-то событие истинно, в противоположность этому логический $0$ означает, что высказывание ложно. Высказывание заменилось на логическое выражение, которое строится из логических переменных ($A$, $B$, $X$, …) и логических операций (связок): ИЛИ, И, НЕ и других.
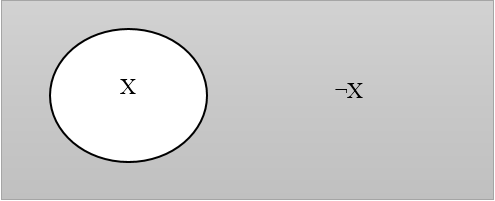
В конце XIX века английский ученый Джордж Венн усовершенствовал круги Эйлера, добавив к изображению объёма рассматриваемого понятия $X$ изображение объёма логически противоположного ему понятия НЕ $X$ (¬$X$). Объём понятия ¬$X$ является дополнением к объёму понятия $X$. Например, дополнение к объему понятия слон является совокупность объектов, которые не являются слонами.
Вклад в развитие логики внесли: Р.Декарт (Франция,1596-1650), Г.Лейбниц (Германия, 1646-1716), М.В.Ломоносов (Россия, 1711-1765), И.Кант (Германия, 1724-1804), О. де Морган (Англия, 1806-1871), Дж. Буль (англия, 1815-1864), Г.Фреге (Германия, 1848-1925), А.А.Марков (Россия, 1903-1979) и многие другие ученые.
В своем развитии логика прошла ряд этапов. Современную логику называют символической или математической логикой. У истоков современной логики стоит Г.Лейбниц, выдвинувший идею представить логическое доказательство как вычисление, подобное математическому вычислению. Он же обосновал необходимость создания универсального математического языка, который мог бы точно и однозначно выражать различные понятия и отношения. Г.Лейбниц пытался разработать своего рода алгебру человеческого мышления, позволяющую получать из уже известных истин новые истины путем точных вычислений.
В современной логике имеются разделы: логика высказываний, логика предикатов и металогика.
Логика высказываний называется формальной логикой. Она основана на «высказываниях». Высказывание - это основной элемент логики, определяемый как повествовательное предложение, относительно которого можно однозначно сказать, истинное или ложное утверждение оно содержит. Вопросительные, побудительные и восклицательные предложения не являютя высказываниями.
Понятие «предикат» обобщает понятие «высказывание». Неформально говоря, предикат – это высказывание, в которое можно подставлять аргументы. Если аргумент один – то предикат выражает свойство аргумента, если больше – то отношение между аргументами. Предикаты записываются в виде некоторого множества символов или сигнатуры, например:

Рисунок 4.
Металогика исследует свойства самих логических систем. К области исследований металогики относятся: формальные языки, формальные системы и их интерпретации. Изучение интерпретации формальных систем есть раздел математической логики, известный как теория моделей, изучение дедуктивного аппарата формальной системы является разделом теории доказательств.












