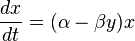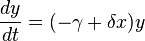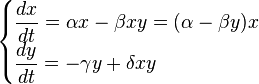Часто представители одного вида (популяции) питаются представителями другого вида.
Модель Лотки – Вольтерры – модель взаимного существования двух популяций типа «хищник – жертва».
Названа в честь авторов модели – Лотка и Вольтерра, которые представили уравнения модели независимо друг от друга. Довольно распространенным является неправильное название – модель Лотки – Вольтерра.
Впервые модель «хищник – жертва» была получена А. Лоткой в 1925 году, который использовал ее для описания динамики взаимодействующих биологических популяций. В 1926 году независимо от Лотки аналогичные (к тому же более сложные) модели были разработаны итальянским математиком В. Вольтерра, глубокие исследования которого в области экологических проблем заложили фундамент математической теории биологических сообществ или т. н. математической экологии.
В математической форме предложенная система уравнений имеет вид:
где x – количество жертв, y – количество хищников, t – время, α, β, γ, δ – коэффициенты, которые отражают взаимодействия между популяциями.
Уравнения используются для моделирования системы «хищник – жертва», «паразит – хозяин», конкуренции и других видов взаимодействия между двумя видами.
Постановка задачи
Рассмотрим закрытое пространство, в котором существуют две популяции – травоядные («жертвы») и хищники. Считается, что животных не ввозят и не вывозят и что еды для травоядных животных достаточно. Тогда уравнение изменения числа жертв (только жертв) примет вид:
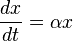
где $α$ – коэффициент рождаемости жертв,
$x$– размер популяции жертв,
$\frac{dx}{dt}$ – скорость прироста популяции жертв.
Когда хищники не охотятся, они могут вымирать, значит, уравнение для количества хищников (только хищников) примет вид:
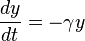
$y$ – размер популяции хищников,
$\frac{dy}{dt}$ – скорость прироста популяции хищников.
При встрече хищников и жертв (частота встреч прямо пропорциональна произведению ) хищники уничтожают жертв с коэффициентом , сытые хищники могут воспроизводить потомство с коэффициентом . Таким образом, система уравнений модели примет вид:
Решение задачи
Построим математическую модель совместного существования двух биологических популяций типа «хищник – жертва».
Пусть две биологические популяции совместно обитают в изолированной среде. Среда является стационарной и обеспечивает в неограниченном количестве всем необходимым для жизни один из видов – жертвы. Другой вид – хищник – также обитает в стационарных условиях, но питается только жертвами. В роли хищников могут выступать коты, волки, щуки, лисы, а в роли жертв – куры, зайцы, караси, мыши соответственно.
Для определенности рассмотрим в роли хищников – котов, а в роли жертв – кур.
Итак, куры и коты живут в некотором изолированном пространстве – хозяйственном дворе. Среда предоставляет курам питание в неограниченном количестве, а коты питаются только курами. Обозначим через
$х$ – количество кур,
$у$ – количество котов.
Со временем количество кур и котов меняется, но будем считать $х$ и $у$ непрерывными функциями от времени t. Назовем пару чисел $х, у)$ состоянием модели.
Найдем каким образом изменяется состояние модели $(х, у).$
Рассмотрим $\frac{dx}{dt}$ – скорость изменения количества кур.
Если котов нет, то количество кур возрастает и тем быстрее, чем больше кур. Будем считать зависимость линейной:
$\frac{dx}{dt} a_1 x$,
$a_1$ – коэффициент, который зависит только от условий жизни кур, их естественной смертности и рождаемости.
$\frac{dy}{dt}$ – скорость изменения количества котов (если нет кур), зависит от количества котов y.
Если кур нет, то количество котов уменьшается (у них нет пищи) и они вымирают. Будем считать зависимость линейной:
$\frac{dy}{dt} - a_2 y$.
В экосистеме скорость изменения количества каждого вида также будем считать пропорциональным его количеству, но только с коэффициентом, зависящим от количества особей другого вида. Так, для кур этот коэффициент уменьшается с увеличением количества котов, а для котов возрастает с увеличением количества кур. Будем считать зависимость также линейной. Тогда получим систему дифференциальных уравнений:
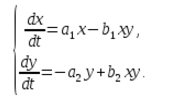
Данная система уравнений называется моделью Вольтерра-Лотки.
a1, a2, b1, b2 – числовые коэффициенты, которые называют параметрами модели.
Как видно, характер изменения состояния модели (x, y) определяется значениями параметров. Изменяя данные параметры и решая систему уравнений модели, можно исследовать закономерности изменения состояния экологической системы.
С помощью программы MATLAB система уравнений Лотки-Вольтерра решается следующим образом:
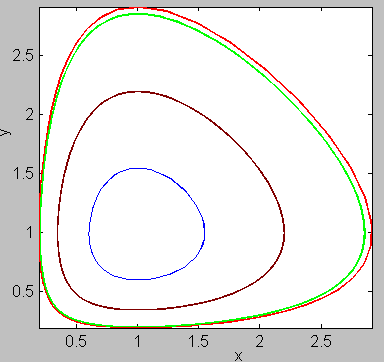
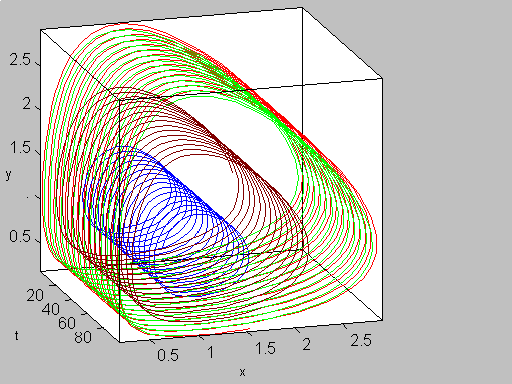
На рис. 1 представлено решение системы. В зависимости от начальных условий решения разные, чему отвечают разные цвета траекторий.
На рис. 2 представлены те же решения, но с учетом оси времени t (т.е. наблюдается зависимость от времени).