Графические модели
Графических моделей достаточно много. Рассмотрим основные из них.
Графы являются наглядным средством отображения состава и структуры системы.
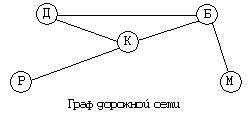
Например, есть словесное описание определенной местности: «Район состоит из пяти поселков: Дорожное, Булавино, Рудино, Крылово и Медвежье. Автомобильные дороги ведут от Дорожного к Булавино, от Дорожного к Крылово, от Булавино к Медвежьему, от Булавино к Крылово, от Крылово к Рудино». По такому описанию очень сложно представить такую местность. Такую информацию гораздо легче воспринимать с помощью схемы. Эта схема не является картой местности, в ней не выдержаны направления по сторонам света, не соблюдается масштаб. На схеме отражены лишь пять поселков и дорожная связь между ними. Схема, которая отображает элементный состав системы и структуру связей, называется графом.
Составными частями графа являются вершины и ребра. Вершины изображаются кругами – это элементы системы, а ребра изображаются с помощью линий – связей (отношений) между элементами. С помощью такого графа можно легко разобраться в структуре дорожной связи данного района.
С помощью данного графа можно легко определить какие поселки нужно проехать, чтобы доехать из Рудино в Медвежье: доступны 2 возможных варианта: 1) Рудино $\to$ Крылово $\to$ Булавино $\to$ Медвежье и 2) Рудино $\to$ Крылово $\to$ Дорожное $\to$ Булавино $\to$ Медвежье. Исходя из данного графа нельзя сделать вывод, что первый путь короче второго, т.к. он не содержит количественных характеристик. Граф не является картой, на которой соблюдается масштаб и присутствует возможность измерить расстояние.
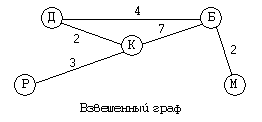
Можно построить граф, который будет содержать количественные характеристики. В таком случае возле ребер графа можно проставить числа, которые обозначают длины дорог в километрах. Такой граф называется взвешенным. Взвешенный граф может содержать количественные характеристики связей и вершин. Например, количественной характеристикой вершины может быть население поселка. По взвешенному графу можно определить, что второй путь короче первого.
Взвешенные графы еще называют сетью. Сеть характеризуется возможностью множества различных путей перемещения по ребрам между некоторыми парами вершин. Сети также характеризуются наличием замкнутых путей, которые называются циклами. На данном графе есть один цикл: Крылово $\to$ Дорожное $\to$ Булавино $\to$ Крылово.
На рассмотренных графах каждое ребро указывает на наличие дорожной связи между двумя пунктами, которая действует одинаково в обе стороны: если по данной дороге можно проехать от Булавино к Медвежьему, то по ней можно проехать и от Медвежьего к Булавино (предполагается, что действует двустороннее движение). Такие графы называются неориентированными, а их связи – симметричными.
Рассмотри граф, который относится к медицине и показывает совместимость групп крови.
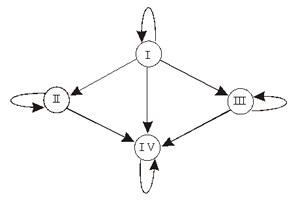
Известно, что кровь каждого человека отличается по группе, которых существует четыре вида. Для переливания крови одного человека другому не все группы подходят. Граф отображает возможные варианты переливания крови. Группы крови – это вершины графа с соответствующими номерами, а стрелки показывают возможность переливания одной группы крови человеку с другой группой крови. Например, по графу можно определить, что кровь I-й группы подходит любому человеку, а человеку с I-й группой крови можно переливать только кровь своей группы; человеку с IV-й группой крови можно переливать любую, а его собственная кровь подходит только человеку с той же группой.
Связи между вершинами данного графа являются несимметричными и поэтому изображены с помощью направленных линий со стрелками. Такие линии называют дугами (а у неориентированных графов – ребрами). Граф с такими свойствами называется ориентированным. Линия, которая выходит и входит в одну и ту же вершину, называется петлей. На данной графе изображены четыре петли.
Таким образом, преимущества изображения модели системы переливания крови в виде графа неоспоримы в сравнении со словесным описанием тех же правил. Граф легко воспринимается и запоминается.
Дерево – граф иерархической структуры
Системы с иерархической структурой являются весьма распространенным типом систем. Иерархическая структура образуется, когда объекты или какие-либо их свойства находятся в отношении подчинения (вложения, наследования). Обычно иерархическая структура присуща системам административного управления, между элементами которых установлены отношения подчиненности. Например: директор организации – начальники отделов – сотрудники. Системы, между элементами которых существуют отношения вхождения одних в другие, также имеют иерархическую структуру.
Граф иерархической структуры называют деревом. Основным свойством такого графа является то, что между любыми двумя его вершинами существует единственный путь. У деревьев нет циклов и петель.
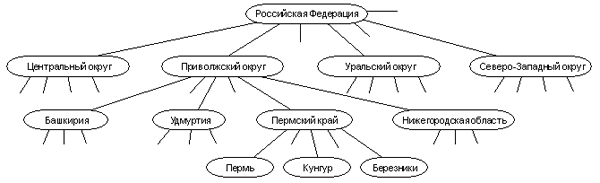
Рассмотрим граф, который отражает иерархическую административную структуру Российской Федерации: государство содержит 7 административных округов; округа делятся на регионы (области и национальные республики), в состав которых входят населенные пункты. Такой граф представляет собой дерево.
Дерево имеет одну главную вершину, называемую корнем дерева. Такая вершина изображается вверху, а от нее проходят ветви дерева. Начиная от корня идет отсчет уровней дерева. Вершины, которые непосредственно связаны с корнем, являются вершинами первого уровня. От них идут ветви к вершинам второго уровня и т.д. Каждая вершина дерева (кроме корня) имеет одну исходную вершину на предыдущем уровне и может иметь множество порожденных вершин следующего уровня. Такой вид связи называется «один ко многим». Вершины, не имеющие порожденных, называются листьями. На данном дереве листьями являются вершины, которые обозначают города.