В рамках метода ЛКАО МО гомо- и гетероядерные двухатомные молекулы рассматриваются аналогично. Основное отличие состоит в том, что для гетероядерных молекул молекулярные орбитали перестают быть симметричными по отношению к плоскости, проходящей через центр тяжести молекулы. Для молекулы типа $АВ$ молекулярные орбитали строят в виде изображения на рис.1.
На рис. 1 схематически изображена система верхних энергетических уровней молекулы $АВ$, которая удовлетворяет следующим требованиям:
1) атом $В$ более электроотрицателен, чем атом $А$,
2) валентные оболочки обоих атомов состоят только из атомных $s-$ и $р-$орбиталей.
Различие в электроотрицательности сводится к тому, что электроны связывающих орбиталей проводят большую часть времени вблизи атома $В$; электронная плотность на разрыхляющих МО, наоборот, смещена в сторону атома $А$. Для использования диаграммы на рис. 1 необходимо определить суммарное число электронов у атомов $А$ и $В$ и затем разместить их по молекулярным орбиталям.
Если молекула $АВ$ состоит из двух разных атомов, то, во-первых, распределение электронной плотности в ней становится несимметричным, а, во-вторых, атомные энергетические уровни слева и справа на рис. 1 становятся неодинаковыми.
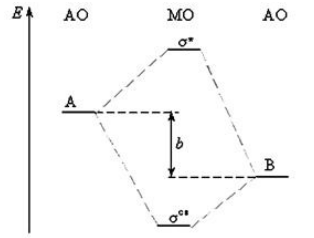
Рисунок 1. Энергии МО для гетероядерных двухатомных молекул
Степень асимметричности связи зависит от природы образующих молекулу атомов. Можно выделить два крайних случая: чисто ковалентную связь и чисто ионную связь. Первая характеризуется совершенно симметричным распределением электронов, как в гомоядерных двухатомных молекулах, а вторая - полным переносом заряда от одного атома к другому. Тогда формулу молекулы лучше записать в виде $А+В-$, а связь между атомами описывать как кулоновское взаимодействие между двумя ионами. Промежуточный между этими крайними случаями асимметричности связи отвечает так называемая полярная связь, для которой характерно неполное смещение электрона от одного атома к другому; в результате у одного из атомов возникает частичный положительный заряд, а у другого - частичный отрицательный заряд. Примером является молекула $HF$, которую можно описать как $H^\sigma+ +F^\sigma-$.
Степень полярности связи
Степень полярности связи рассчитывают или из экспериментальных данных, например, из дипольных моментов, или из детальных молекулярно-орбитальных расчетов. Однако приблизительно полярность связей можно оценить из таблицы электроотрицательности элементов, в которой способность атома притягивать электроны обозначают числом. Существует несколько таблиц электроотрицательности, но самой известной является таблица Полинга (табл. 1).

Рисунок 2.
В квантовой механике каждая МО строится из атомных орбиталей путем их линейной комбинации. В общем, любая связывающая МО записывается выражением:
$\Psi=C_А \varphi_А + C_В \varphi_В$, где $\varphi_А$ и $\varphi_В$ - атомные орбитали, при взаимодействии которых образуется данная молекулярная орбиталь, а $C_А$ и $C_В$ - коэффициенты, с которыми они входят в МО. Доля $\varphi_А$ в рассматриваемой МО равна квадрату коэффициента $C_А$, т.е. $C_А^2$, а доля $\varphi_В$ равна $C_В^2$. По условию нормировки сумма квадратов коэффициентов должна быть равна единице. Для чисто ковалентной связи $C_А^2=C_В^2=\frac{1}{2}$, поскольку $C_А^2+C_В^2=1$, а для чисто ионной связи $А^+ В^- C_А^2=0$ и $C_В^2=1$. Для полярной молекулы $А^{\sigma+} В^{\sigma-} C_А^2\frac{1}{2}$.
Рассмотрим полярную молекулу HF
Связь между атомами $Н$ и $F$ в этой молекуле образуется перекрыванием орбиталей $Н_2s$ и $F_2s$, однако коэффициенты, с которыми эти орбитали входят в линейную комбинацию, в результате которой образуется связывающая $\sigma$-МО, не одинаковы, а именно $C_F >C_H$. Схематически это можно изобразить, используя «кружки» или «восьмерки» (в случае р-орбиталей) разных размеров; радиусы можно взять пропорциональными $C_F$ и $C_H$ в молекуле $H^{\sigma+} F^{\sigma-}$, тогда площади будут пропорциональны $C_F^2$ и $C_H^2$.
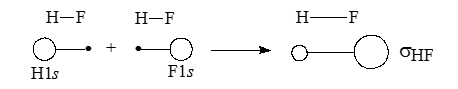
Рисунок 3.
Приведенная упрощенная схема показывает, что плотность связывающей $\sigma$-орбитали в молекуле $HF$ больше на атоме $F$, чем не атоме $Н$. В действительности картина связывания атомов в молекуле $HF$ несколько сложнее, поскольку возможно не только перекрывание $s$-орбиталей, но и перекрывание между орбиталями $H_1s$ и $F_2p$:

Рисунок 4.
Такое перекрывание увеличивает плотность орбитали между атомами $H$ и $F$, что ведет к понижению энергии молекулы. Однако в основном связь между $H$ и $F$ обеспечивается перекрыванием $s$-орбиталей (рис. 5).
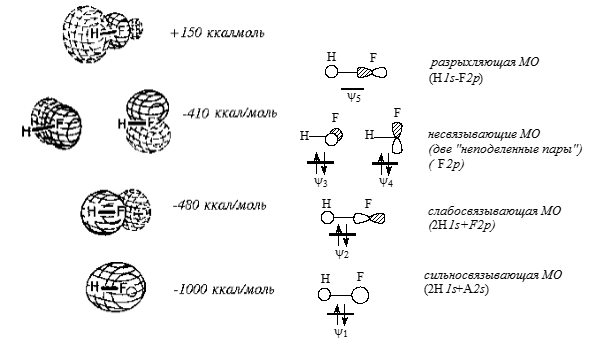
Рисунок 5. МО молекулы $HF$
На рис. 5 дана форма МО простейшей двухатомной гетероядерной молекулы $HF$. Поскольку валентная оболочка атома фтора описывается одной $2s-$ и тремя $2р-$атомными орбиталями, а атом водорода имеет $1s-$орбиталь, общее число образующихся молекулярных орбиталей в молекуле равно пяти. На четырех нижних по энергии орбиталях $\Psi 1- \Psi 4$ попарно размещаются восемь электронов, пятая орбиталь пустая. На рисунке, кроме объемных изображений МО, приведены также эскизы орбиталей, дающие представление о симметрии и о том, какие АО атома фтора использованы для образования данной МО.











