Из экспериментов известно, что сильнее всего рассеивается коротковолновое излучение (фиолетовый и синий свет). Это явление в XIX веке объяснил Рэлей. Основным положением, от которого отталкивался ученый, стало то, что в центрах рассеяния под воздействием электромагнитной волны появляются вынужденные колебания, частота которых равна частоте волны. В таком случае центр рассеивания можно считать микро диполем, совершающим колебания, соответственно, излучающим вторичные волны. Дипольный момент такого диполя равен:
где $E_0{cos \left(\omega t\right)\ }$ -- член, определяющий колебания напряженности электрического поля волны коллинеарной оси $Z$ в плоскости $Y=0$, $m$ -- масса электрона, $q_e$ -- его заряд, ${\omega }_0$ -- собственная частота колебаний электрона, которая определяется силой упругости, которая удерживает электрон в положении равновесия.
При этом поле вторичной волны, которую излучает диполь можно определить в сферической системе координат (пусть полярная ось совпадает с направлением диполя) как:
где $\theta ,\varphi $ -- полярный и аксиальный углы, $r-$расстояние от диполя до точки, в которой определяется поле.
Плотность потока энергии (вектор Умова - Пойнтинга) в направлении, которое характеризуем углами ($\theta \ и\ \varphi $) равна:
Усредним выражение (3) по периоду, учтем выражение (1), получаем:
Часто от частоты переходят к длине волны, используя соотношение:
В таком случае формула (4) запишется как:
Поток энергии $dW(\theta ,\varphi )$ в телесный угол $d\Omega =\frac{d\sigma }{r^2},$ который опирается на элемент площади $d\sigma $ равен:
Интенсивность рассеяния ($I_1(\theta ,\varphi )$) определена как:
Надо отметить, что выражение (8) задает плотность энергии рассеянного потока от одного элементарного излучателя. Данное выражение чаще представляют в виде:
где $\left\langle P_0\right\rangle $ -- среднее значение потока энергии в падающей волне.
В том случае, если размеры рассеивателя много меньше длины волны, то все элементарные диполи излучают когерентно. Под рассеянием Рэлея понимают рассеяние молекулами вещества, следовательно, их размер обычно много меньше длины волны видимого света. Элементарные рассеиватели относят к разным молекулам, они излучают некогерентно. Учитывая вышесказанное, сделаем вывод о том, что интенсивность рассеянной волны от одной молекулы увеличивается пропорционально квадрату количества элементарных рассеивателей ($N_0$) в ней. Если концентрацию молекул обозначить как N. Тогда в единице объема содержится $NN_0$ элементарных диполей. Используя известное соотношение:
где $n$ -- показатель преломления вещества. Подставим в (9) левую часть формулы (10) вместо соответствующего выражения, получим интенсивность рассеяния от одной молекулы:
Полученная формула справедлива, когда собственная частота ${\omega }_0$ много больше частот видимого света и ближнего ультрафиолета. Если все частоты электронов одинаковы, то полная интенсивность рассеяния одной частицей по всем направления равна:
Для вычисления интенсивности рассеяния в единице объема используют при рассеянии в неплотных газах формулу:
Соответственно это выражение можно преобразовать и получить зависимость $I_V$ от частоты:
Так, Рэлей показал, что при прочих равных условиях интенсивность света, рассеиваемого частицей пропорциональна четвертой степени частоты волны света или обратно пропорциональна четвертой степени длины волны (закон Рэлея).
Угловая диаграмма направленности
Из формулы Рэлея следует, что интенсивность света связана с углом рассеяния.
Можно представить интенсивность рассеянного света в зависимости от угла рассеяния:
где $\varphi -\ $угол рассеивания, $N\ $ -- концентрация рассеивающих объектов$\ (молекул),\ \ $ Изменение интенсивности симметрично относительно первоначальному распространению пучка света. Кривая, которая представляет распределение интенсивности рассеянного света от угла рассеяния, называется индикатрисой рассеяния. Угловое распределение интенсивности рассеяния для поляризованного света показано на рис.1.
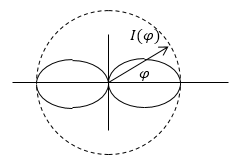
Рисунок 1.
Длина отрезка $I\left(\varphi \right),$ который отсекается на индикатрисе, определяет относительную интенсивность рассеяния в избранном направлении.
Во сколько раз сильнее будут рассеиваться в воздухе ультрафиолетовые лучи (${\lambda }_1\approx 0,05мкм$), если сравнить их с инфракрасными лучами (${\lambda }_2\approx 5мкм$)?
Решение:
Объемный коэффициент молекулярного рассеяния (${\sigma }_m$), который выделяют в законе Рэлея можно определить как:
\[{\sigma }_m=const\frac{{\left(n-1\right)}^2}{N{\lambda }^4}\left(1.1\right),\]где $N$ -- концентрация рассеивающих частиц. Из (1.1) найдем искомое отношение:
\[\frac{{\sigma }_{m1}}{{\sigma }_{m2}}=\frac{{\lambda }^4_2}{{\lambda }^4_1}.\]Проведем вычисления:
\[\frac{{\sigma }_{m1}}{{\sigma }_{m2}}={\left(\frac{5}{0,5}\right)}^4={10}^{-4}.\]Ответ: Ультрафиолетовые волны рассеиваются в ${10}^4\ $раз сильнее, чем инфракрасные.
Из формулы Рэлея $I_V=\frac{32{\pi }^3{{{\varepsilon }_0}^2(n-1)}^2}{3N{\lambda }^4}\left\langle P_0\right\rangle $ кажется, что интенсивность рассеянного света обратно пропорциональна концентрации рассеивающих частиц, тогда как следовало бы предположить что яркость рассеянного света будет больше с увеличением концентрации центров рассеяния. Как объяснить сложившуюся ситуацию?
Решение:
Рассмотрим закон Рэлея:
\[I_V=\frac{32{\pi }^3{{{\varepsilon }_0}^2\left(n-1\right)}^2}{3N{\lambda }^4}\left\langle P_0\right\rangle \left(2.1\right).\]В числителе мы видим показатель преломления ($n)$ , который сам пропорционален концентрации ($n\sim N$). Показатель преломления возведен в квадрат, получается, что как и следовало ожидать $I_V\sim N.$ Интенсивность рассеянного света тем больше, чем выше концентрация рассеивающих частиц.











