Основой электродинамики в неподвижных средах является система уравнений Дж Максвелла. Эти уравнения получены последовательной систематизацией, интеграцией и исследованием эмпирических фактов. Прежде всего, необходимо решить, какие из известных ранее уравнений могут быть оставлены без изменений и оговорок, какие из них требуют обобщения, трансформации или вообще требуется отбросить. В качестве ориентира в этом отношении используют следующее положение: исключаются из состава основных все уравнения, в основе которых лежат представления о непосредственном действии на расстоянии. К таким законам относят, например, закон Кулона, Био и Савара. Эти законы не совмещаются с пониманием того, что электромагнитные взаимодействия распространяются с конечной скоростью, следовательно, не являются верными в абсолютно всех случаях. Сохраняют только те уравнения, которые не противоречат положениям теории поля.
В качестве гипотезы предполагается, что теорема Остроградского -- Гаусса:
уравнение:
закон электромагнитной индукции (в формулировке Максвелла):
являются общими законами электродинамики. То, что они удовлетворяют требованиям теории поля, следует из существования этих же законов в дифференциальной (полевой) трактовке:
К основным уравнениям электродинамики добавляют закон сохранения заряда, который в дифференциальной форме представлен как:
В случае стационарности электромагнитного поля выражение (5) переходит в:
Теорема о циркуляции:
может быть также записана в дифференциальной форме:
следовательно, удовлетворяет требованиям теории поля. Тем не менее, она не входит в состав основных уравнений электродинамики. Если в выражении (8) провести операцию дивергенции для обеих частей равенства, то получим, что $div\overrightarrow{j}=0$, так как $div(rot\overrightarrow{H)}=0$. Однако, выражение (6) справедливо только для стационарных токов. Получается, что мы получено противоречие с уравнением (5) для общего случая. Полагать, что не выполняется закон (5) нельзя, так как это фундаментальный закон сохранения заряда. Значит, следует сделать вывод, что выражения (7) и (8) требуют обобщения. Это обобщение вводится в виде тока смещения. Плотность тока смещения ($\overrightarrow{j_{sm}}$) определена как:
Максвелл назвал плотностью полного тока выражение $\ \overrightarrow{j}+\overrightarrow{j_{sm}}$ , причем:
Максвелл переписал выражение (8) в виде:
Доказательством истинности уравнения (11) служат опытные данные, которые подтверждают уравнение (11).
Итак, Максвелл дополнил основные положения электромагнетизма введением токов смещения и написал систему фундаментальных уравнений электродинамики. В настоящее время их четыре. В дифференциальной форме эта система имеет вид:
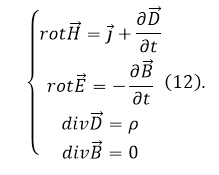
Рисунок 1.
В число фундаментальных уравнений не включено уравнение непрерывности (5), так как это уравнение -- следствие уравнений, которые входят в систему Максвелла.
Уравнения Максвелла показывают, что источниками электрического поля служат электрические заряды и переменные магнитные поля. Магнитные поля порождаются перемещающимися электрическими зарядами (токами) и переменными электрическими полями. Уравнения Максвелла не являются симметричными относительно магнитного и электрического полей. Это произошло вследствие того, что электрические заряды в природе существуют, а магнитных зарядов считается, что не существует. Дирак, в свое время, стремясь придать уравнениям электродинамики симметрию, выдвинул гипотезу о существовании магнитных зарядов, назвал их единичными магнитными полюсами (монополиями). Логических противоречий этой гипотезе нет. Существование таких зарядов потребовало бы обобщения уравнений Максвелла. Потребовалось бы к источникам магнитного поля добавить магнитные заряды, а к источникам электрических полей -- магнитные токи. При этом справедливость уравнений Максвелла была бы ограничена областями, в которых магнитных зарядов и магнитных токов нет. Однако попытки экспериментального обнаружения магнитных зарядов по сей день успехом не увенчались.
Рассуждения, с помощью которых получена система уравнений Максвелла, не может служить доказательством. Принципиально новые положения старая теория никогда не содержит. В этом смысле нельзя вывести уравнения Максвелла логически. Данные уравнения следует рассматривать как основные аксиомы электродинамики, которые получены путем обобщения эмпирических данных.
Задание: Объясните, в чем разница между пониманием явления электромагнитной индукции Максвеллом и Фарадеем?
Решение:
Согласно представлениям Фарадея, электромагнитная индукция состоит в том, что переменное магнитное поле возбуждает электрический ток. Для того чтобы наблюдать это явление, обязательно требуется замкнутый проводник.
Максвелл видел суть электромагнитной индукции прежде всего в порождении электрического поля, следовательно, это явление можно наблюдать, когда в пространстве нет проводников вообще. И возникновение электрического тока в проводнике -- одно из проявлений электрического поля, которое появляется как следствие изменения магнитного поля. Это поле может выполнять и другие действия, например, поляризовать диэлектрик, ускорять заряженные частицы. Предположение Максвелла подтверждают эксперименты, которые показывают, что ЭДС индукции не зависит от рода и состояния проводника (его температуры, однородности). Это показывает, что причиной возникновения ЭДС заключается в появлении электрического поля под действием переменного магнитного поля, и проводник играет второстепенную роль и является детектором поля.
Важная особенность явления в том, что появляющееся электрическое поле не является электростатическим. Электрическое поле, которое появляется при электромагнитной индукции, имеет непрерывные линии напряженности (обладает вихревым характером). Циркуляция вектора напряженности в таком поле отлично от нуля зависит от формы проводящего контура. Углубленное истолкование явления электромагнитной индукции ведет к основному положению теории Максвелла о том, что переменное магнитное поле вызывает появление вихревого электрического поля. Что количественно отображается в уравнении:
\[rot\overrightarrow{E}=-\frac{\partial \overrightarrow{B}}{\partial t}.\]Задание: Что представляет собой система уравнений Максвелла для стационарных полей?
Решение:
В том случае, если мы рассматриваем стационарное магнитное и стационарное электрическое поля, то следует учесть, что:
\[\frac{\partial \overrightarrow{D}}{\partial t}=\frac{\partial \overrightarrow{B}}{\partial t}=0\ \left(2.1\right).\]В таком случае, система уравнений Максвелла распадется на две группы независимых уравнений. Первая группа -- уравнения электростатики:
\[rot\overrightarrow{E}=0,\ div\overrightarrow{D}=\rho \ \left(2.2\right).\]Вторая группа -- уравнения магнитостатики:
\[rot\overrightarrow{H}=\overrightarrow{j},\ div\overrightarrow{B}=0\ \left(2.3\right).\]В случае стационарных полей электрическое и магнитное поля независимы друг от друга. Источниками электрического поля являются только электрические заряды, источники магнитного поля -- токи проводимости.











