Теорема Карно
Еще в 1848 г. В. Томсон отметил, что теоремой Карно можно воспользоваться, чтобы построить рациональную температурную шкалу, которая не зависит от особенностей термометрического вещества и устройства термометра.
Поэтому прежде чем перейти непосредственно к рассмотрению термодинамической шкалы температур, сформулируем теорему, которая называется теоремой Карно:
КПД ($\eta $) тепловой машины можно рассчитать по формуле:
\[\eta =1-\frac{Q_{ch}}{Q_n}\ \left(1\right),\]где $Q_n$ - количество теплоты, полученное рабочим телом от нагревателя, $Q_{ch}$- количество теплоты, отданное рабочим телом холодильнику. Так как $\eta $ имеет одинаковые значения для всех тепловых машин, работающих по обратимому циклу Карно с температурой нагревателя и температурой холодильника. Обозначим временно величины этих температур ${\theta }_1\ и\ {\theta }_2,$ то для отношение $\frac{Q_{ch}}{Q_n}$ можно записать:
\[\frac{Q_{ch}}{Q_n}=f\left({\theta }_1\ ,\ {\theta }_2\right)\left(2\right),\]где $f\left({\theta }_1\ ,\ {\theta }_2\right)$ - функция температур холодильника и нагревателя, универсальная для всех циклов Карно. Покажем, что $f\left({\theta }_1\ ,\ {\theta }_2\right)$ можно представить в виде:
\[f\left({\theta }_1\ ,\ {\theta }_2\right)=\frac{\varphi \left({\theta }_1\right)}{\varphi \left({\theta }_2\right)}\ \left(3\right),\]где $\varphi \left(\theta \right)$ - универсальная функция от температуры.
Отношение двух термодинамических температур
Рассмотрим две обратимые машины (рис.1). Холодильник одной машины -- нагреватель для другой. Допустим, что вторая машина отбирает от нагревателя с температурой ${\theta }_2$- столько тепла, сколько отдает ему первая машина (${Qch}_2={Qn}_2$). Исходя из (2), для каждой машины запишем:
\[\frac{Q_{ch2}}{Q_{n1}}=f\left({\theta }_1\ ,\ {\theta }_2\right)\left(4\right),\] \[\frac{Q_{ch3}}{Q_{ch2}}=f\left({\theta }_2\ ,\ {\theta }_3\right)\left(5\right).\]Если рассмотреть машину на рис.1 как единую с тепловым резервуаром температуры (${\theta }_1$) и холодильником с температурой (${\theta }_3$), то получим:
\[\frac{Q_{ch3}}{Q_{n1}}=f\left({\theta }_1\ ,\ {\theta }_3\right)\left(6\right).\]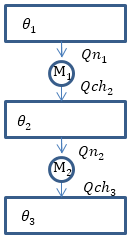
Рис. 1
Разделим (6) на (4), имеем:
\[\frac{Q_{ch3}}{Q_{ch2}}=\frac{f\left({\theta }_1\ ,\ {\theta }_3\right)}{f\left({\theta }_1\ ,\ {\theta }_2\right)}=\frac{Q_{n2}}{Q_{ch2}}\left(7\right).\]Сравниваем (7) и (5), получаем:
\[f\left({\theta }_2\ ,\ {\theta }_3\right)=\frac{f\left({\theta }_1\ ,\ {\theta }_3\right)}{f\left({\theta }_1\ ,\ {\theta }_2\right)}\ \left(8\right).\]Уравнение (8) связывает температуры, связывает все температуры${\ \theta }_1\ ,\ {\theta }_2,\ {\theta }_3.$ Решим, что ${\ \theta }_1$ постоянна, получим, что функция $f\left({\theta }_1\ ,\ \theta \right)$ -- функция одной переменной $\theta $. Обозначим эту функцию $\varphi (\theta )$, тогда уравнение (8) примет вид:
\[f\left({\theta }_2\ ,\ {\theta }_3\right)=\frac{\varphi \left({\theta }_3\ \right)}{\varphi \left({\theta }_2\ \right)}\ \left(9\right),\]или
\[f\left({\theta }_1\ ,\ {\theta }_2\right)=\frac{\varphi \left({\theta }_2\ \right)}{\varphi \left({\theta }_1\ \right)}\ \left(10\right),\]Что совпадает с тем, что мы хотели доказать, то есть с выражением (3).
Функция $\varphi \left(\theta \ \right)$ зависит только от температуры. Поэтому ее значение можно использовать для характеристики температуры соответствующего тела, то есть полагать температуру равной $\varphi $, где $\varphi =\varphi \left(\theta \ \right).$ В таком случае уравнение (4) примет вид:
\[\frac{Q_{ch2}}{Q_{n1}}=\frac{{\varphi }_2}{{\varphi }_1}\ \left(11\right).\]Соотношение (11) ложится в основу термодинамической шкалы температур. Ее преимущество -- независимость от выбора рабочего тела в цикле Карно, которое используют для измерения температуры.
Величину $\varphi $ принимают за меру температуры тела и называют абсолютной термодинамической температурой. В примерах мы покажем, что она совпадает с используемой нами ранее с абсолютной температурой T по шкале идеального газового термометра. В выражении (11) мы видим отношение двух термодинамических температур. Чтобы определить температуру одного тела можно:
- взять какие-либо две постоянные температурные точки (например, температуру плавления льда $T_i$ при нормальных условиях и температуру кипения воды ($T_k$)). Найти разность количества теплоты кипения $(Q_k)$ и плавления $(Q_i)$, допустим, что разность ${(Q}_k-Q_i)=100$ градусам, тогда температурный интервал делим на 100 равных частей, каждая часть кельвин. Решаем систему из двух уравнений: \[\frac{T_k}{T_i}=\frac{Q_k}{Q_i},\ T_k-T_i=100\ (12)\]
- Второй метод: для сопоставления температур двух тел необходимо осуществить цикл Карно, в котором исследуемые тела использовать, как нагреватель и холодильник. Отношение, отданное теплоты к полученной теплоте -- есть отношение температур исследуемых тел.
вычисляем температуры. Отношение теплот можно измерить или найти косвенным вычислением.
Абсолютная термодинамическая температура не может быть отрицательной. Самая низкая температура, которую допускает второе начало термодинамики: T=0K. Абсолютная термодинамическая шкала температур тождественна с абсолютной шкалой.
Задание: Докажите тождественность термодинамической шкалы температур с абсолютной шкалой идеального газового термометра, используя цикл Карно. В качестве рабочего тела рассмотрите 1 моль идеального газа.
Решение:
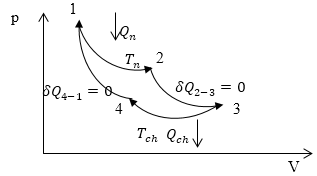
Рис. 2
Найдем количество теплоты, которое получило рабочее тело. Поступление теплоты происходит на изотермическом участке 1-2.
\[Q_n=\int\limits^{\left(2\right)}_{\left(1\right)}{\delta Q}=\int\limits^{\left(2\right)}_{\left(1\right)}{dU}+\int\limits^{\left(2\right)}_{\left(1\right)}{pdV}=RT_nln\frac{V_2}{V_1}\left(1.1\right),\]Первый интеграл равен нулю, так как мы имеем дело с изотермическим процессом, а второй -- работе при $T_n=const$ (которая рассчитывалась в разделе изотермический процесс). На участке 3-4 система тепло отдает в холодильник при температуре $T_{ch}$. Запишем $Q_{ch}$:
\[Q_{ch}=RT_{ch}ln\frac{V_4}{V_3}\left(1.2\right).\]Найдем отношение:
\[\frac{Q_{ch}}{Q_n}=\frac{RT_{ch}ln\frac{V_4}{V_3}}{RT_nln\frac{V_2}{V_1}}\left(1.3\right).\]Выясним, как соотносятся отношения объемов. Для этого используем уравнения адиабат для соответствующих процессов в цикле Карно:
\[T_1V^{\gamma -1}_2=T_2V^{\gamma -1}_3,\ T_1V^{\gamma -1}_1=T_2V^{\gamma -1}_4\to \frac{V_2}{V_1}=\frac{V_3}{V_4}\to {ln \left(\frac{V_2}{V_1}\right)\ }={ln \left(\frac{V_3}{V_4}\right)\ }\left(1.4\right).\]Соответственно выражение (1.3) будет иметь вид:
\[\frac{Q_{ch}}{Q_n}=\frac{T_{ch}}{T_n}\left(1.5\right).\]Сравниваем уравнение (1.5) с выражением, которое было получено для отношения термодинамических температур (1.6):
\[\frac{Q_{ch}}{Q_n}=\frac{{\varphi }_2}{{\varphi }_1}\ \left(1.6\right).\]Можно сделать вывод о том, что абсолютная термодинамическая шкала температур станет тождественной с соответствующей температурной шкалой идеального газового термометра, если в обоих случаях температуре основной реперной точки приписать одно и тоже значение. Так как на практике так и поступают, то считаем, что тождественность $\varphi =T$ доказана.
Задание: Докажите, что термодинамическая температура не может быть меньше нуля.
Решение:
Пусть тело с температурой $T_{ch} \[\eta =1-\frac{T_{ch}}{T_n}\left(2.1\right),\]
если $T_{ch}0,\ $ получается $\eta >1$, что противоречит второму началу термодинамики, следовательно, неосуществимо.











