Гетерогенное состояние
Состояние системы, в котором в равновесии находятся несколько фаз, называется гетерогенным. Такое равновесие возможно, если температуры, давления и химические потенциалы фаз одинаковы.
Пусть в систему входит K компонент, и эта система находится в A -- фазах, в таком случае вопрос о количестве независимых параметров, которые необходимы для однозначного описания системы, решает правило, которое получил Гиббс и которое носит его имя.
Допустим, что наша система находится при постоянных давлении и температуре, в таком случае условие равновесие для каждой фазы запишем в виде:
\[{\left(dФ\right)}_{T,p}=\sum\limits_i{d{\mu }_in_i}=0\ \left(1\right),\]где $Ф=H-TS=U+pV-TS$ -- энергия Гиббса (изобарно -- изотермический потенциал), ${\mu }_i$- химический потенциал компоненты с номером i, $n_i$- концентрация i -- компоненты системы. Общее количество уравнений вида (1) равно числу фаз А. Всего в эти уравнения входит $(K\cdot A)$ величин ${\mu }_i$, но не все из них являются независимыми. Так как состав каждой фазы не изменяется, то возникает одна связь между химическими потенциалами, соответственно таких условий-связей всего (А). Химические потенциалы каждой компоненты во всех фазах должны быть одинаковы, то есть:
\[{\mu }_{i1}={\mu }_{i2}=\dots ={\mu }_{iА}\left(2\right).\]Для каждого i есть A-1 равенство, для всех компонент получается K(A-1) условие. Из вышесказанного следует, что количество независимых ${\mu }_i$ равно:
\[K\cdot A-A-K\left(A-1\right)=K-A\ \left(3\right).\]Конечно, давление и температура так же являются независимыми параметрами. Получается, что количество независимых параметров ($f$), которые необходимы для однозначного описания системы, которая состоит из K компонент и находится в A фазах, запишется так:
\[f=K-A+2\ \left(4\right),\]Вспомним, что идеальный газ мы описывали с помощью двух параметров, например, давления и температуры, а объем находили из уравнения состояния. Уравнение (4) называется правилом фаз Гиббса.
Возможна ситуация, когда на равновесие системы влияют не только такие внешние параметры как давление и температура, а, например, электрические поля, магнитные поля и т.д. В этом случае внешних факторов буде не 2 как в (4), а B (в общем случае), тогда выражение запишется как:
\[f=K-A+B\ \left(5\right),\]где B -- количество внешних независимых параметров.
Иногда, например, так часто делают в металлургии при рассмотрении конденсированных систем можно считать давление постоянным, и влиянием его пренебрегают, в таком случае считается, что правило фаз Гиббса записывается:
\[f=К+1-A\left(6\right).\]Другими словами, можно сказать, что если какой либо из внешних параметров системы фиксируется, (например условием p=const или T=const), то выполняется правило фаз в виде (6).
Выражения (4), (5), (6) показывают, что число степеней свободы не может быть отрицательным, не имеет физического смысла. Так как $f\ge 0$, то число существующих фаз системы удовлетворяет неравенству:
\[A\le K+2\ \left(7\right).\]Неравенство (7) означает, что число фаз, которые могут находиться в равновесии между собой не может превышать число компонент более чем на две. Это утверждение еще одна формулировка правила фаз Гиббса.
В однокомпонентной системе $1\le A\le 3$. При $A=3,\ f=0$, это означает, что может равновесно существовать три фазы вещества (к примеру, газ, жидкость и твердое вещество) только в одном определенном состоянии, которое называют тройной точкой.
Правило фаз Гиббса
Согласно правилу Гиббса получается, что с увеличением количества компонентов в системе, увеличивается число степеней свободы, с другой стороны, если увеличивается количество фаз системы, уменьшается число необходимых переменных.
Правило фаз Гиббса применяется в металлургии, химических технологиях, материаловедении. Оно позволяет рассчитать число фаз в многокомпонентных системах и число термодинамических степеней свободы.
Если в многофазной системе происходят химические реакции, необходимо учитывать количество химических уравнений. В состав таких уравнений войдут уравнения связи концентраций веществ, уравнения материального баланса. Дополнительные уравнения следует вычесть из правой части уравнения (4) или просто учесть через количество компонентов. Использовать $K'=K-l$ вместо K, где $l$ -- число дополнительных уравнений.
Задание: Определить $А,\ K\ и\ f$ для системы жидкость -- ее пар используя правило Гиббса. Как на термодинамической диаграмме отображается состояние такой системы?
Решение:
Так как в условии сказано, что система жидкость и ее пар, то количество имеющихся фаз -- две. Это значит, что A=2, система имеет одну компоненту K=1. Тогда в соответствии с правилом Гиббса количество уравнений, однозначно описывающих состояние системы, будет равно:
\[f=K-A+2\ \left(1.1\right).\]Подставляем соответствующие величины, получаем:
\[f=1-2+2=1.\]Так как количество уравнений, которое необходимо, для описания системы равно одному, то на термодинамической диаграмме, например в осях (p,T) однокомпонентная система из двух фаз будет изображена как линия АК (фазовая диаграмма перехода жидкости в пар рис. 1).
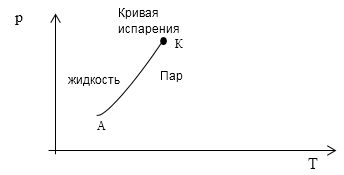
Рис. 1
Ответ: $А=2,\ K=1\ и\ f=1$. Состояние такой системы отображается кривой на фазовой диаграмме рис. 1.
Задание: Чему равно число степеней свободы трехфазного состояния системы с одной компонентой. Что можно сказать о параметрах такой системы в состоянии равновесия?
Решение:
В соответствии с правилом фаз Гиббса, запишем:
Система имеет одну компоненту: K=1, фазы в системе три, следовательно A=3, найдем число необходимых уравнений f по правилу Гиббса:
\[f=K-A+2\ \left(2.1\right).\]Проведем подстановку данных:
\[f=1-3+2=0\]Ответ: Так как $f=0$ это означает, что три фазы однокомпонентной системы могут находиться в равновесии только при единственном соотношении параметров системы. Такая точка называется тройной на термодинамической диаграмме. На диаграмме в тройной точке пересекаются кривые плавления, испарения и сублимации.











