Что такое испарение
Испарением называется процесс парообразования, который происходит со свободной поверхности жидкости.
Испарение происходит при любой температуре и происходит интенсивнее с увеличением температуры. В результате испарения происходит охлаждение жидкости, так как испарение можно объяснить тем, что молекулы, обладающие наибольшей кинетической энергией, вылетают с поверхностного слоя жидкости, преодолевая силы притяжения соседних молекул. Скорость испарения зависит от внешнего давления и движения газообразной фазы над свободной поверхностью жидкости. С повышением температуры плотность, следовательно, давление насыщенного пара над жидкостью увеличиваются. При увеличении плотности паров, поверхностное натяжение жидкости уменьшается, следовательно, скрытая теплота парообразования с повышением температуры уменьшается. При критической температуре (${\ T}_k$) плотность насыщенных паров равна плотности жидкости, различие между этими фазами вещества исчезает. Получается, что при критической температуре поверхностное натяжение и скрытая теплота парообразования равны нулю. Пар, строго говоря, газом не является. У паров близких к насыщению давление незначительно изменяется в зависимости от объема. Газовые законы, могут приближенно применяться к ненасыщенным парам.
Что такое кипение
Процесс интенсивного испарения жидкости не только с ее свободной поверхности, но и по всему объему жидкости внутрь образующихся в процессе пузырьков пара называют кипением.
Давление p внутри пузырька пара определяют в соответствии со следующим выражением:
\[p=p_0+\rho gh+p_{R\ }\left(1\right),\]где $p_0$- внешнее давление, $\rho gh$- давление слоев жидкости, которые расположены выше, $p_{R\ }=\frac{2\sigma}{r}$ -- дополнительное давление, которое вызвано с кривизной пузырька, $r$- радиус пузырька, $h$ - расстояние от центра пузырька до поверхности жидкости, $\rho $ -- плотность жидкости, $ \sigma $ -- поверхностное натяжение жидкости.
Кипение начинается тогда, когда давление (упругость) насыщенного пара внутри пузырька ($p_p$) больше чем давление в правой части формулы (1). Если жидкость имеет центры парообразования, то кипение жидкости начинается при более низких температурах. Если $\rho gh\ll p_0$, то можно считать, что кипение начинается при $p_p\approx p_0$. Температуру жидкости, при которой давление ее насыщенного пара равно внешнему давлению, называют температурой (точкой) кипения (${\ T}_k$). Строго говоря, кипение на различных уровнях жидкости происходит при различных температурах, нет какой то одной определенной температуры. Определенную температуру имеет насыщенный пар, который находится над поверхностью кипящей жидкости. Его температура не зависит от того как происходит кипение в глубине жидкости, и определяется только внешним давлением. Именно температура такого пара имеется в виду, когда говорят о температуре кипения.
Если кипение происходит при постоянном давлении ($p_0$), то температура кипения постоянна. Тепло, подводимое к системе, в таком случае расходуется только на парообразование.
Что такое конденсация
Процесс, обратный испарению, называют конденсацией.
При конденсации тепло выделяется. Кипение жидкости, конденсация пара -- фазовые переходы первого рода. Напомним, что фазовым переходом первого рода называют переход, который сопровождается скачкообразным изменением внутренней энергии и плотности вещества. При фазовых переходах первого рода, к которым относятся испарение и конденсация, термодинамический потенциал (Ф) системы не изменяется.
Количество теплоты, которое необходимо израсходовать при парообразовании единицы массы жидкости при температуре равной ${\ T}_k$, называют удельной теплотой парообразования (или скрытой теплотой кипения) ($r_k$). Удельную теплоту парообразования можно найти из уравнения Клайперона -- Клаузиуса:
\[r_k=\left(v_p-v_j\right)T_k\frac{dp}{dT_k}\left(2\right),\]где $v_p,v_j$ -- удельные объемы пара и жидкости при температуре кипения $T_k$. Соответственно, зависимость температуры кипения от давления в процессе испарения определяется как:
\[\frac{dT_k}{dp}=\frac{\left(v_p-v_j\right)T_k}{r_k}\ \left(3\right).\]Так как $v_p>v_j$ и $r_k>0$, то $\frac{dT_k}{dp}>0.\ $ На рис 1. представлена кривая фазового равновесия процесса парообразования. Она заканчивается в критической точке К. Следствием обрыва кривой испарения в точке К является непрерывность жидкого и газообразного состояния вещества. Температура кипения растет при увеличении давления.
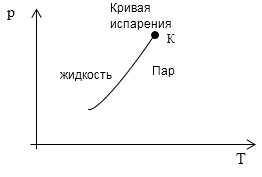
Рис. 1
Задание: Определите молярную теплоту испарения жидкости при температуре T и давлении p насыщенных паров, если жидкость и ее пар подчиняются уравнению Ван-дер-Ваальса. Коэффициенты в уравнении Ван-дер-Ваальса равны a и b, $T\ll T_k$.
Решение:
Теплота парообразования, исходя из первого начала термодинамики, может быть вычислена как:
\[r_p=U_p-U_j+p\left(V_p-V_j\right)\left(1.1\right),\]где $U_j-$ внутренняя энергия жидкости, $U_p$ внутренняя энергия пара, $V_j,V_p$ объемы жидкости и пара соответственно, $p\left(V_p-V_j\right)-\ работа,\ совершаемая\ при\ испарении$ против сил внешнего давления p. Разность внутренних энергий по уравнению Ван-дер-Ваальса равна:
\[U_p-U_j=\frac{a}{V_j}-\frac{a}{V_p}\left(1.2\right).\]используем уравнение Ван-дер-Ваальса для одного моля вещества:
\[\left(p+\frac{a}{V^2}\right)\left(V-b\right)=RT\to p=\frac{RT}{\left(V-b\right)}-\frac{a}{V^2}\ \left(1.3\right).\]Получаем:
\[r_p=\frac{a}{V_j}-\frac{a}{V_p}+p\left(V_p-V_j\right)=V_p\left\{\frac{RT}{V_p-b}-\frac{2a}{V^2_p}\right\}-V_j\ \left\{\frac{RT}{V_j-b}-\frac{2a}{V^2_j}\right\}\ (1.4).\]Ответ: Молярная теплота испарения жидкости при заданных условиях равна: $r_p=V_p\left\{\frac{RT}{V_p-b}-\frac{2a}{V^2_p}\right\}-V_j\ \left\{\frac{RT}{V_j-b}-\frac{2a}{V^2_j}\right\}$.
Задание: Два килограмма воды взяли при температуре 00C при атмосферном давлении нагрели и превратили в пар полностью. Найдите изменение энтропии, если считать процесс обратимым.
Решение:
В качестве основы для решения задачи возьмем определение энтропии для обратимого процесса:
\[\triangle S=\int{\frac{\delta Q}{T}}=\triangle S_{nagr}+\triangle S_p\ (2.1),\]где $\triangle S_{nagr}$ изменение энтропии при нагревании воды от нуля по Цельсию до температуры кипения, то есть от $T_1=273\ K\ до\ T_2=373\ K$. $\triangle S_p-\ $изменение энтропии при парообразовании. Найдем изменение энтропии при нагревании воды:
\[\triangle S_{nagr}=\int\limits^{T_2}_{T_1}{\frac{\delta Q}{T}}=\int\limits^{T_2}_{T_1}{\frac{cmdT}{T}}=cm\int\limits^{T_2}_{T_1}{\frac{dT}{T}}=cmln\left(\frac{T_2}{T_1}\right)\left(2.2\right),\]где $c$ удельная теплоемкость воды равна $c=4,2\ {\cdot 10}^3\frac{Дж}{кгК}$
Процесс парообразования при температуре кипения идет без изменения температуры, поэтому выражение для изменения энтропии в этом процессе будет иметь вид:
\[\triangle S_p=\frac{1}{T_2}\int{\delta Q}=\frac{1}{T_2}\triangle Q=\frac{r_pm}{T_2}\left(2.3\right),\]где $r_p$- удельная теплота парообразования из справочных материалов равна для воды $r_p=22,6\cdot {10}^5\frac{Дж}{кг}$.
Окончательно выражение для изменения энтропии имеем в виде:
\[\triangle S=cmln\left(\frac{T_2}{T_1}\right)+\frac{r_pm}{T_2}\ \left(2.4\right).\]Все данные переведены в СИ, проведем расчет:
\[\triangle S=4,2\ {\cdot 10}^3\cdot 2{ln \left(\frac{373}{273}\right)\ }+\frac{22,6\cdot {10}^5\cdot 2}{373}=14,6{\cdot 10}^3\frac{Дж}{К}.\]Ответ: Изменение энтропии в заданном процессе равно $1,46{\cdot 10}^4\frac{Дж}{К}$.












