
Зависимость намагниченности от температуры магнетика
Обменную энергию (Wob) для ферромагнетика можно записать как:
где →S1→S2 -- спины, электронов, которые взаимодействуют, Iob -- интеграл обменного взаимодействия. При Iob>0 энергия взаимодействия минимальна в случае параллельных спинов. Она вызвана взаимодействием магнитного момента электрона (→pm) с магнитным полем (индукция обменного поля →Bob) и определяется формулой:
Собственный магнитный момент электрона (→pm0) связан со спином →S соотношением:
где qe, m -- заряд и масса электрона. Разделим и умножим правую часть выражение (1) на qem, получим:
Положим, что второй электрон находится в магнитном поле, которое создает первый электрон, тогда следует записать:
Суммарная индукция магнитного поля складывается из индукции поля без обменного взаимодействия (→B) и индукции обменного поля (→Bob). Используя известные соотношения:
получим:
где →J -- вектор намагниченности, ϰ -- магнитная восприимчивость, μ -- магнитная проницаемость, μ0 -- магнитная постоянная, →H -- напряженность магнитного поля.
Если присутствует обменное взаимодействие, то формулу (10) можно обобщить до:
Пусть величина λ -- постоянная обменного взаимодействия, тогда можно считать, что:
Подставим (12) в (11), получим:
Произведем замену:
где ϰ′ характеризует восприимчивость с учетом обменного взаимодействия (ϰ=CT).
При T>λC вещество ведет себя как парамагнетик. Магнитная восприимчивость уменьшается при увеличении температуры. При T=λC в соответствии с (15) ϰ′→∞. Этот факт значит, что самые малые магнитные поля вызывают конечную намагниченность. Или иначе, при T=λC возникает спонтанная намагниченность, то есть парамагнетик переходит в ферромагнетик. Более точные теоретические изыскания показывают, что спонтанная намагниченность при T=λC возникает скачком, и при уменьшении температуры возрастает. То есть при $T
Температура Кюри. Закон Кюри -- Вейсса
Для любого ферромагнетика существует температура (Tk) при которой области спонтанной намагниченности распадаются и вещество теряет ферромагнитные свойства и становится парамагнетиком. Такая температура называется точкой Кюри (или температурой Кюри). Она для разных ферромагнетиков может существенно различаться. Так для железа TkFe=768∘C, для никеля TkNi=365∘C.
Магнитная восприимчивость ферромагнетика подчиняется закону Кюри -- Вейсса:
где величина λC=θ называется температурой Кюри -- Вейсса. Теория показывает, что фазовый переход осуществляется не при температуре Кюри -- Вейсса, а близкой к ней. Иногда не делают различий между температурой Кюри, при которой происходит фазовый переход и температурой Кюри --Вейсса.
Задание: Используя функцию Ланжевена, покажите область спонтанной намагниченности ферромагнетика. Как связана спонтанная намагниченность и температура ферромагнетика?
Решение:
Из теории Ланжевена можно получить для ферромагнетиков два следующих уравнения:
J=JnL(x) (1.1),где Jn -- намагничивание насыщения, k -- постоянная Больцмана, b -- постоянная Вейсса, x=pm(H+bJ)kT, pm -- магнитный момент. Первое уравнение удобно представить кривой Ланжевена (OAA0) (рис.1). Уравнение (1.2) -- прямая СА, которая пересекает вертикальную ось в точке C, ордината которой в точке C равна -Hb.
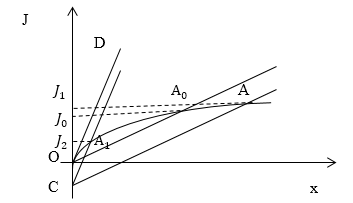
Рис. 1
Если температура ферромагнетика меньше температуры Кюри для него (T\[kTnJnbВтакомслучаепрямаяACпересечеткривуюЛанжевенавточкеА,ординатаэтойточкиестьнамагниченностьферромагнетика(J_1).Еслиуменьшатьнапряженностьвнешнегомагнитногополя,тоточкаC,будетподниматьсякточкеО,аточкаАперемещатьсякточкеA_0.ЕслиH=0,тонамагниченностьравнаJ_{0.}$ При температуре ниже точки Кюри ферромагнетик спонтанно намагничен. Энергии теплового движения молекул не достаточно, чтобы нарушить спонтанное намагничивание.
Допустим, что наклон прямой СА больше наклона кривой Ланжевена, то есть T>Tk. При наличие внешнего магнитного поля прямая СА займет положение ОD, то есть пересечет кривую Ланжевена только в начале координат, где намагничивание равно нулю. Спонтанное намагничивание отсутствует, намагничивание разрушается тепловым движением.
Задание: Используя функцию Ланжевена, получите закон Кюри -- Вейсса.
Решение:
Используем рис.1 (Пример 1). Рассмотрим ферромагнетик при температуре T>Tk. Спонтанное намагничивание отсутствует. Для того чтобы намагнитить вещество, необходимо приложить внешнее магнитное поле. Рассчитаем намагничивание. Прямая АС при этом займет положение СЕ и будет пересекать кривую Ланжевена в точке A1.Ордината точки A1 будет определять намагниченность тела (J2). Ордината ОС, полученная эмпирически равна -Hb, она мала, следовательно участок ОA1 кривой Ланжевена, так же мал. Значит, участок ОA1 можно считать отрезком прямой, и написать:
L(x)=(dLdx)x=0x (2.1),получим:
J=Jn(dLdx)x=0x (2.2).если ввести для температуры Кюри выражение:
Tk=Jn2bkn(dLdx)x=0(2.4).получим:
J=ϰH (2.5),где
ϰ=Tkb(Т−Tk)=СТ−Tk (2.6),где С=const. Уравнение (2.6) -- закон Кюри -- Вейсса.



















