Уже в древности появились первые приспособления, при помощи которых поднимали и передвигали большие тяжести, приводили в действие осадные орудия (тараны) и т. д. Все эти приспособления служили для того, чтобы вызывать такие движения, при которых необходимо преодолевать большие силы (например, при подъеме тяжелого груза его вес). Иными словами, можно считать, что силы, развиваемые приспособлениями, должны быть равны по величине и противоположны по направлению силам, противодействующим движению. Все такие приспособления называют простыми машинами. Таким образом, вопрос о действии простых машин сводится к определению условий, при которых простая машина находится в равновесии.
Еще в древности при применении простых машин (рычаг, тачка, блок, ворот и т. д.) была обнаружена замечательная особенность всех этих машин: оказалось, что в простых машинах перемещения вполне определенным образом связаны с силами, развиваемыми машиной. Именно отношение перемещений двух концов простой машины, к которым приложены силы, всегда обратно отношению сил, приложенных к этим концам.
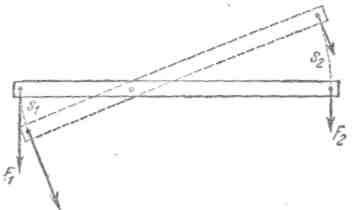
Рис. 1. Выигрыш в силе и проигрыш в перемещении на примере рычага.
Например, если для равновесия рычага сила $F_1$ должна быть в n раз больше, чем сила $F_2$ (рис. 1), то при вращении рычага перемещение $S_1$ его первого конца будет в n раз меньше, чем перемещение $S_2$ второго конца. Для двойного блока такое же соотношение получается между силами, приложенными к веревкам, намотанным на оба блока и удерживающим его в равновесии, и перемещениями концов веревок при вращении блока. Это обстоятельство было сформулировано еще в древности следующим образом: «то, что мы выигрываем в силе, мы проигрываем в пути». Положение это имеет столь общее и вместе с тем столь важное значение, что оно получило название «золотого правила» механики.
Пользуясь введенными обозначениями, можем выразить «золотое правило» следующей формулой: $\frac{F_2}{F_1}=\frac{S_1}{S_2}$.
«Золотое правило» механики практически соблюдается только в тех случаях, когда движение простых машин происходит равномерно или с малыми ускорениями. Например, при вращении двойного блока концы веревок, навитых на скрепленные между собой блоки радиусов $r_1$ и $r_2$, переместятся на расстояния $S_1$ и $S_2$, пропорциональные этим радиусам: $\frac{S_1}{S_2}=\frac{r_1}{r_2}$
Значит, для того, чтобы «золотое правило» было справедливо для двойного блока, должно быть выполнено условие $\frac{F_2}{F_1}=\frac{r_1}{r_2}$. Тогда силы $F_1$ и $F_2$ уравновесятся и, значит, машина должна либо покоиться, либо двигаться равномерно. Но для того, чтобы привести в движение двойной блок, нужно нарушить равновесие, прибавив к одной из сил, например к $F_1$, некоторую силу $f$ (рис. 2). Возникающее движение будет ускоренным. При этом «золотое правило» не соблюдается: $(F_1+f)$ $S_1 $>$F2S2$. Но чем меньше сила $f$ по сравнению с $F_1$ тем меньше отклонение от «золотого правила». При очень малых $f$ движение будет происходить с очень малым ускорением, т. е. будет близко к равномерному.
Итак, «золотое правило» механики соблюдается вполне точно при равномерном движении (без трения) и приближенно при движении с малым ускорением. Ни одна машина не движется всегда равномерно: вначале она должна прийти в движение, а в конце должна остановиться. Но если пуск в ход и остановка двойного блока происходят с малым ускорением, то «золотое правило» механики практически справедливо во все время действия этой машины.
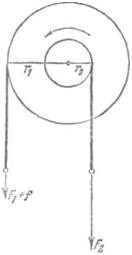
Рис. 2. Блок вращается с ускорением.
Таким же образом, как и для двойного блока, мы могли бы убедиться, что «золотое правило» механики справедливо и для всех простых машин при условии, что направления приложенных к машине сил и направления перемещений точек приложения сил совпадают. Для всех таких машин «золотое правило» механики справедливо в том виде, как мы вывели его для двойного блока: при равномерном движении машины (а практически также при движении с очень малыми ускорениями) произведения силы на перемещение точки приложения для обеих сил равны.
Длинное плечо рычага $l_1=2м$, короткое $l_2=0,5м$. Какое усилие потребуется приложить при подъёме груза массой т=100 кГ к концу длинного плеча рычага?
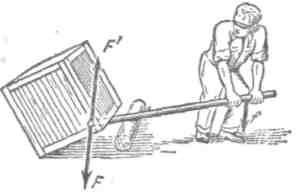
Рис. 3. Применение рычага
Решение
Равновесие рычага наступает при условии, что отношение приложенных к его концам параллельных сил обратно отношению плеч и моменты этих сил противоположны по знаку. Согласно «золотому правилу механики», $\frac{F_2}{F_1}=\frac{l_1}{l_2}$, откуда $F_1=F_2\frac{l_2}{l_1}=mg\frac{l_2}{l_1}=100\cdot 9.81\cdot \frac{0.5}{2}=245\ H$
Для подъёма ведра из колодца используется двойной блок (рис.4)
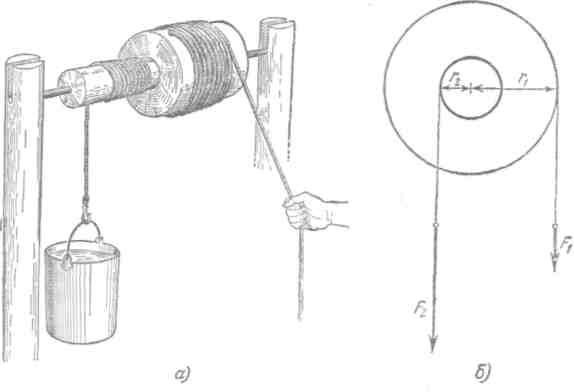
Рис. 4. а) Двойной блок, б) Схема двойного блока.
Радиусы блока $r_1$ = 0,5 м и $r_2$ =0,25 м. Вес ведра с водой 10 кГ. Какое усилие надо приложить к верёвке , чтобы система была в равновесии?
Решение
Для двойного блока справедливо «золотое правило», поэтому выполняется условие $\frac{F_2}{F_1}=\frac{r_1}{r_2}$. Отсюда получаем $F_1=F_2\frac{r_2}{r_1}=mg\frac{r_2}{r_1}=10\cdot 9,81\cdot \frac{0,5}{0,25}=\ $19,6 H











