Клин - это разновидность простого механизма «наклонная плоскость». Он имеет призматическую форму и состоит из двух плоскостей, которые сходятся под острым углом. Его применяют, чтобы получить выигрыш в силе, то есть при помощи меньшей силы противодействовать большей силе.
При рубке дров, чтобы облегчить работу, в трещину полена вставляют металлический клин и бьют по нему обухом топора.
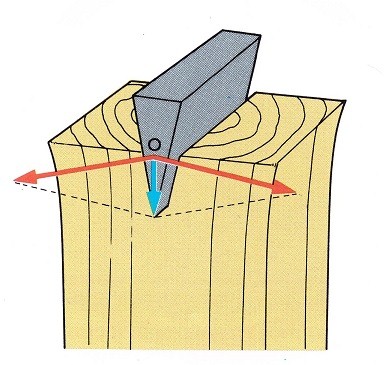
Рисунок 1. Раскалывающее действие клина
При забивании клина в дерево наклонные плоскости развивают боковые силы, достаточные для расщепления самых прочных пиломатериалов.
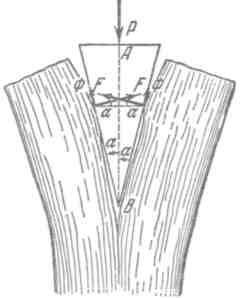
Рисунок 2 Силы, действующие на клин при рубке дров
На тыльную поверхность клина, например при ударах кувалды, действует сила $Р$, вгоняющая клин в трещину (рис. 2); на боковые поверхности клина действуют силы давления $F$ со стороны раскалываемого полена. При равновесии клина сумма проекций всех приложенных к нему сил на любое направление, например на ось клина, должна равняться нулю, т. е. сила $Р$ должна уравновешивать сумму составляющих сил $F$, направленных вдоль оси клина.
Проекция силы $F$ на АВ равна $Fsin\alpha $. На рис.2 изображен клин, симметричный относительно плоскости АВ: стороны клина составляют с АВ одинаковые углы $\alpha $, и обе проекции сил равны. В таком случае условие равновесия клина есть $P=2Fsin\alpha $. При малом $\alpha $ сила $Р$ может быть значительно меньше $2F$. Например, для топора-колуна, представляющего собой стальной клин на рукоятке, угол лезвия равен около 25${}^\circ$ (2$\alpha $ =25${}^\circ$); в соответствии с этим $Р$ примерно в пять раз меньше, чем $2F$.
Идеальный выигрыш в силе, даваемый клином, равен отношению его длины к толщине на тупом конце - расклинивающее действие клина даёт выигрыш в силе при малом угле и большой длине клина. Реальный выигрыш клина сильно зависит от силы трения, которая меняется по мере хода клина.
Клин известен людям уже более 9000 лет. В Древнем Египте бронзовые клинья использовались в карьерах для откалывания каменных блоков, необходимых в строительстве. Также применялись деревянные клинья, которые разбухали после обливания водой.
Клинья и сейчас широко используются нами в повседневной жизни для того, чтобы поднимать тяжёлые объекты и отделять их от поверхности, на которой они лежат. Они могут также использоваться для раскалывания предметов. Узкий и относительно длинный клин может применяться для точной подгонки просвета между предметами (обычно применяют плотники).
Клинья также могут быть использованы для удержания предметов, таких как части двигателя или другого механизма. Широко применяются и дверные клинья, которые блокируют дверь из-за трения между нижней частью двери и клином и между клином и поверхностью.
Принцип клина используется в таких инструментах и орудиях, как топор, зубило, нож, гвоздь, игла, кол.
Сила $P$, прилагаемая к торцу клина шириной $S$ = 9 см, равна 4000 Н. Длина клина $l$ = 10.8 см. Определить величину раскалывающей силы, с которой действует на полено боковая поверхность клина, если к.п.д. клина 20%.
Решение
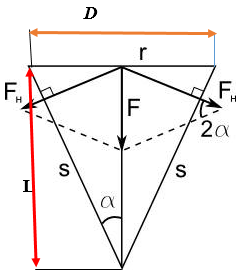
Рисунок 3
Дано:
$P$ = 4000 H
$D =2r$ = 9 см
$L$ = 10.8 см
${\mathbf \eta }$ = 0.2
$F_н$ - ?
Сила $Р$, прилагаемая к торцу клина, расходуется на преодоление трения и на раскалывание полена. Работу по раскалыванию совершает сила $\overrightarrow{\ F}=\eta \overrightarrow{P}$ Раскалывающее действие боковой поверхности клина равно по величине и противоположно по направлению силе, с которой полено давит на боковую поверхность: $F=\ \eta P=2F_н{sin \alpha \ }$. Учитывая, что ${sin \alpha \ }=\frac{r}{S}=\frac{D}{\sqrt{D^2+4L^2}}$, получим: $F_н=\frac{\eta P\sqrt{D^2+4L^2}}{2D}=\frac{0.2\cdot 4000\cdot \sqrt{9^2+{4\cdot 10.8}^2}}{2\cdot 9}=1040\ H\ $
Ответ: $F_н=1040\ H$
На гладкой горизонтальной плоскости находится клин с углом $\alpha $ при основании. Тело массы $m$, положенное на клин, опускается с ускорением, направленным под углом $\beta $ $>$ $\alpha $ к горизонтали (рис. 4). Определите массу клина.
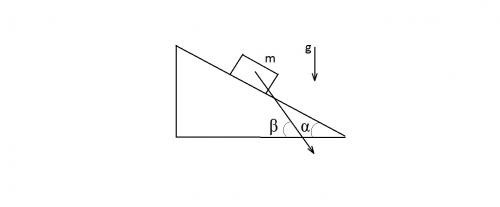
Рисунок 4
Решение
Разложим ускорение тела $а_0$ в горизонтальном направлении $a_1$ и вдоль наклонной плоскости (рис. 5):
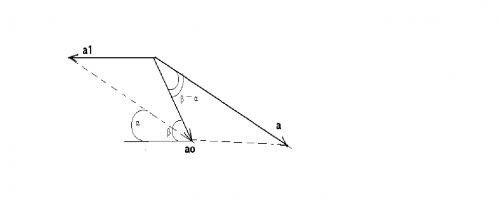
Рисунок 5
По теореме синусов: $a1 / sin({\mathbf \beta }$ - ${\mathbf \alpha })$ = $a / sin({\mathbf \pi }$ - ${\mathbf \beta }$), где $a_1$ - ускорение клина, которое возникает под действием тела, а точнее, под действием силы инерции $F = ma cos {\mathbf \alpha }$. Т.е. $Ma_1 = ma cos {\mathbf \alpha }$. Подставляя значение ускорения, получим $Ma•sin({\mathbf \beta }$ - ${\mathbf \alpha }$)/sin ${\mathbf \beta }$ = $macos$${\mathbf \alpha }$
Откуда находим массу клина:
$M = m tg$ ${\mathbf \alpha }$ / (tg ${\mathbf \beta }$ - tg ${\mathbf \alpha }$).
Ответ: Масса клина $M = m tg$ ${\mathbf \alpha }$ / (tg ${\mathbf \beta }$ - tg ${\mathbf \alpha }$)












