Дифференциальный блок состоит из двойного блока и одного простого блока и использует бесконечную цепь (рис. 1,а). Цепь, переброшенная через большой неподвижный блок радиусом $R$, охватывает нижний подвижный блок. Второй конец цепи обёрнут вокруг малого неподвижного блока радиусом $r$. Неподвижные блоки образуют ступенчатый барабан, дающий выигрыш в силе в удвоенном отношении радиуса большего блока к разности радиусов неподвижных блоков. Чтобы цепь не скользила по блокам, в них делают углубления для звеньев цепи. На рис. 1,б показана схема сил для дифференциального блока.
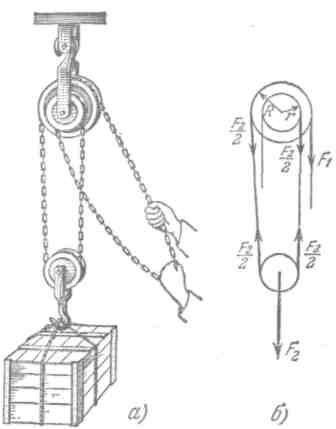
Рис. 1. а) Дифференциальный блок б) Схема дифференциального блока
Условие равновесия диифференциального блока: $F_1R=\frac{1}{2}F_2\left(R-r\right)$
Мы видим, что в условие равновесия входит разность радиусов двух блоков. Поэтому система и названа дифференциальным (разностным) блоком.
При расчетах блоков необходимо учитывать потерю энергии на трение, или коэффициент полезного действия блокa.
Для неподвижного блока к. п. д. равен 0,96, для подвижного блока 0,97, для талей 0,80, для дифференциального блока до 0,5.
Дифференциальный блок (рис.2) состоит из двух скреплённых между собой и насаженных на общую горизонтальную ось О барабанов с радиусами $r_1$ = 9 см и $r_2$ = 13 см В устройстве обеспечены условия непроскальзывания троса по барабанам. Найдите минимальную силу $F$, которую необходимо приложить к тросу, чтобы поднимать груз массой $m$= 65 кг. Массой подвижного блока пренебречь.
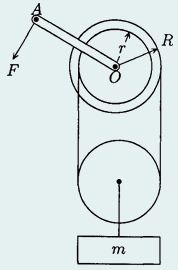
Рисунок 2
Решение
Дано:
$m$ = 65 кГ
$R$ = 0,13 м
$r$ = 0,09 м
${\mathbf \eta }$ = 0,5
$g$ = 9,8 $м/c_2$
$F$ - ?
Согласно условию равновесия дифференциального блока, $F=mg\frac{R-r}{2R\eta }=65\cdot 9,8\cdot \frac{0,13-0,09}{2\cdot 0,13\cdot 0,5}=196\ H$
Ответ: Для подъёма груза достаточно приложить силу 196 Н
Дифференциальный блок имеет диаметр большой звездочки 320 мм, а малой 300 мм. Какой груз можно поднять таким блоком, приложив усилие 490 Н?
Решение
Дано:
$F$ = 490 H
$R$ = 0,32 м
$r$ = 0,3 м
${\mathbf \eta }$ = 0,5
$g$ = 9.8 $м/c_2$
$m$ - ?
Согласно условию равновесия дифференциального блока,
$mg\left(R-r\right)=2\eta FR$, откуда
\[m=2\eta F\frac{R}{g\left(R-r\right)}=2\cdot 0.5\cdot 490\cdot \frac{0.32}{9.8\cdot \left(0.32-0.3\right)}=800\ кг\]Ответ: Приложенной силы достаточно для подъёма груза массой 800 кг.











