
Закон Мозли
В начале $XX$ века Мозли эмпирическим путем выявил важную связь длин волн спектральных линий характеристического рентгеновского излучения и номером химического элемента в системе Менделеева. Закон Мозли можно записать в виде:
где ${\nu }^*=\frac{1}{\lambda }$ -- волновой число линий, $R=10973731\ м^{-1}$ -- постоянная Ридберга, $a\ {\rm и}\ у$ некоторые постоянные, которые характеризуют серию линий рентгеновского характеристического спектра и вещество антикатода.
В частности, для длин волн $K_{\alpha }-\ $линии характеристического рентгеновского спектра закон Мозли принимает вид:
Выражение (2) можно представить в виде:
где $\sigma =1$, $m=1,\ n=2.$
Соотношение (4) сходно с формулой для длины волны линии серии Лаймана для водородоподобного иона. Отличие в том, что параметр $Z^2$, который входит в формулы серий для водородоподобных систем, в выражении (4) уменьшен на величину постоянной $\sigma $. Величина $\sigma $ называется постоянной экранирования, которая в данном случае равна единице. Постоянная экранирования отражает тот факт, что в тяжелом атоме, который имеет $Z$ электронов, на электрон выполняющий переход, отвечающий линии $K_{\alpha }$, воздействует не целиком заряд ядра ($Zq_e$), а величина $(Z-1)q_e$. То есть заряд ослаблен экранирующим действием одного электрона, который остался в слое $K$.
На рис.1 изображена диаграмма Мозли, которая отображает линейную зависимость $\sqrt{\frac{{\nu }^*}{R}}$ от номера химического элемента $Z$ для линии $K_{\alpha }$.
Использование закона Мозли в применении к атомам химических элементов периодической системы стало подтверждением закономерного роста заряда ядра на единицу при переходе от одного элемента к следующему. Это послужило доказательством истинности ядерной модели атома и объяснения теории периодической системы.
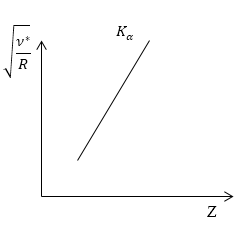
Рисунок 1.
Общий вид рентгеновского терма можно представить:
В таком случае закон Мозли запишем как:
Выражение (6) показывает то, что квадратные корни из рентгеновских термов линейно связаны с зарядовым числом элемента ($Z$).
Если электрон был выбит из $K$- оболочки ($n=1$), то в результате перехода на освободившееся место электронов с других оболочек происходит излучение рентгеновской $K$ -- серии. При переходе электронов на освобожденное место в оболочке $L$ ($n=2$) происходит излучение $L$ -- серии и так далее. Можно сделать вывод о том, что одинаковая структура рентгеновских спектров и закон Мозли являются подтверждением истинности периодической системы элементов.
Примеры задач
Какой химический элемент длину волны для линии ${\ K}_{\alpha }$ линейчатого спектра рентгеновского излучения получилась равную $72пм$? Считать постоянную $\sigma =1$.
Решение:
Чтобы ответить на вопрос задачи следует найти атомный номер элемента в системе Д.И. Менделеева. Для решения задачи используем закон Мозли в виде:
\[\frac{1}{\lambda }={R\left(Z-1\right)}^2\left(\frac{1}{1^2}-\frac{1}{2^2}\right)или\] \[\frac{1}{\lambda }={R\frac{3}{4}\left(Z-1\right)}^2\left(1.1\right),\]где $R=10973731\ м^{-1}.$ Выразим параметр $Z$ из формулы (1.1), имеем:
\[{\left(Z-1\right)}^2=\frac{4}{3лR}\ \to Z=\sqrt{\frac{4}{3лR}}+1.\]Проведем вычисления, если $\lambda =72пм=7,2\cdot {10}^{-11}м$:
\[Z=\sqrt{\frac{4}{3\cdot 7,2\cdot {10}^{-11}\cdot 1,1\cdot {10}^7}}+1=42\]Ответ: $Z=42$, следовательно это молибден.
Какова постоянная экранирования ($\sigma $) для $L$ -- серии характеристического рентгеновского излучения, если длина волны, которая испускается при переходе электрона с $M$ -- оболочки на $L$ -- оболочку составила $140 \ пм$ (рис 2).?
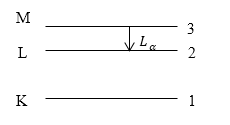
Рисунок 2.
Решение:
Запишем численные данные необходимые для решения задачи, так, атомный номер вольфрама, взятый из периодической системы $Z=74$.
В качестве основы для решения задачи используем закон Мозли, записанный в виде:
\[\frac{1}{\lambda }={R\left(Z-\sigma \right)}^2\left(\frac{1}{m^2}-\frac{1}{n^2}\right)\left(2.1\right),\]где $m=2,\ n=3$, так как образуется $L_{\alpha }$ -- линия. Тогда упростим формулу (2.1) до выражения:
\[\frac{1}{\lambda }=\frac{5}{36}{R\left(Z-\sigma \right)}^2\left(2.2\right).\]Выразим из формулы (2.2) постоянную экранирования:
\[{\left(Z-\sigma \right)}^2=\frac{36}{5лR}\ \to \sigma =Z-\sqrt{\frac{36}{5\lambda R}.}\]Проведем вычисления, учитывая, что $\lambda =140пм=1,4\cdot {10}^{-10}м,\ R=10973731\ м^{-1}$:
\[\sigma =74-\sqrt{\frac{36}{5\cdot 1,4\cdot {10}^{-10}\cdot 1,1\cdot {10}^7}}\approx 5,62.\]Ответ: $\sigma =5,62.$










