Синглетные состояния
Расщепление энергетических уровней в результате спин-орбитального взаимодействия называют тонкой структурой. Систему подуровней, на которые расщепляется исследуемый уровень, называют мультиплетом. Количество подуровней, на которые расщепляется уровень, определяет название мультиплета: дублет, триплет, квартет, квинтет и так далее. Уровни, которые не расщепляются, называют синглетами. Аналогичные термины используют для именования совокупностей линий спектра.
Анализ термов в спектрах щелочных металлов показывает, что $s$ -- термы $(l=0)$ являются синглетами, так как суммарный (полный) момент (внутренне квантовое число) (в единицах $\hbar $) ($\overrightarrow{j}=\overrightarrow{l}+\overrightarrow{s}$) для $s$ -- термов допускается только $j=s=\frac{1}{2}>0$.
То, что $s$- уровни никогда не расщепляются, то есть всегда являются синглетными, связывают с особенностями перемещения электронов в $s$ -- состоянии. В таком состоянии электронное облако имеет сферическую симметрию относительно ядра. При этом движение радиально, так как орбитальный момент равен нулю. Значит в $s$ -- состоянии спин -- орбитального взаимодействия нет, и соответствующие энергоуровни являются синглетными.
Синглетом может именоваться совокупность двух частиц, результирующий спин которой равен нулю. Так, например, при комбинации $2$ электронов, каждый из которых имеет спин равный $\frac{1}{2}$ можно получить три состояния с результирующим спином равным: единице (триплет), а также одно состояние с суммарным нулевым спином (синглет). Спиновые функции для подобной системы из $2$ электронов можно представить как линейную комбинацию спиновых функций электронов (${\gamma }_s-симметричная\ функция,$ ${\gamma }_a$ -- антисимметричная функция):
где ${\alpha }_1=\frac{1}{2}\hbar ,\ {\alpha }_2=-\frac{1}{2}\hbar $ - спиновые функции электронов.
Антисимметричная функция дает синглет со спином равным нулю. Волновая функция электронной подсистемы молекулы - произведение пространственной и спиновой волновых функций. При этом полная волновая функция электронной подсистемы представляется в виде произведения пространственной и спиновой волновых функций. Симметричной пространственной функции соответствует антисимметричная спиновая функция (синглетное состояние).
В обозначениях Дирака собственное состояние вида (2) записывают как:
Синглетные состояния описывает антисимметричная спиновая функция.
Триплетные состояния
В состояниях возбуждения неспаренные электроны спины электронов могут быть параллельными или антипараллельными. Если молекула обладает четным числом электронов, тогда возможно два варианта возбужденного состояния, которые отличны по мультиплетности: синглет и триплет. Триплетное состояние описывает симметричная спиновая волновая функция (1) и антисимметричная пространственная функция. Так как электроны отталкиваются энергия синглетного состояния выше, чем аналогичного триплетного состояния, при той же конфигурации электронов.
Если мы имеем две частицы со спином равным $\frac{1}{2}$, то можно получить три собственных состояния, результирующий спин которого равен $1$ -- это будет триплет. Используя обозначения Дирака собственные состояния запишем как:
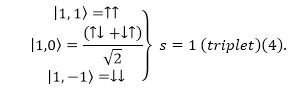
Рисунок 1.
На математическом языке говорят, что тензорное произведение двух дублетов можно разложить в сумму триплета и синглета. Триплетные энергетические состояния расположены ниже, чем синглеты. Переход из синглетного возбуждения в триплетное называют интеркомбинационной конверсией. Данная молекулярная реакция внутри молекулы идет в месте пересечения кривых с потенциальной энергией синглета и триплета. При данной конверсии ориентация спина фотоэлектрона изменяется на противоположную. Как результат, спины двух раньше спаренных электронов становятся параллельными. При наличии внешнего магнитного поля триплетный уровень расщепляется на три составляющих уровня. Каждый из них отвечает одному типу ориентации суммарного спина (по полю и против него, перпендикулярно полю).
Правило отбора в квантовой механике запрещает переход из синглетного состояния в триплетное. При этом работает спиновый запрет и запрет по симметрии. Но, надо отметить, что в результате спин -- орбитального взаимодействия (спинового магнитного момента фотоэлектрона и орбитального момента) в состоянии триплета имеется примесь синглетного состояния. При этом вероятность перехода синглет -- триплет существенное увеличивается (особенно при наличии тяжелых атомов).
Отметим, что триплетный терм состоит из трех состояний, тогда как для синглета понятия синглета и терма являются тождественными. Допустим, что мы имеем ион подобный гелию с электронной конфигурацией: $1snp$. В приближении $LS$ -- связи для заданной конфигурации мы имеем термы: ${}^1{P,\ }{}^3{P.\ }$ Состояниями заданных термов являются: ${}^1{P_1;\ {}^3{P_{0,1,2}.\ }\ }$ Так, триплет состоит из трех состояний, синглет -- из одного, то есть понятия терма и состояния являются тождественными.
Задание: Каков основной терм атома углерода, каково его основное состояние?
Решение:
Атом углерода имеет электронную конфигурацию вида:
\[1s^22s^22p^2.\]На внешней оболочке имеем два электрона. Максимально возможный суммарный спин будет равен:
\[S=1.\]Получаем, что основной терм будет триплетом. В соответствии с правилом Хунда нам следует выбрать максимальное из возможных значение $L$ для двух одинаковых p-электронов. При этом будем следовать принципу Паули. Рассмотрим все варианты возможных квантовых чисел, которые опишут состояния электронов:

Рисунок 2.
При этом числа выберем так, что сначала должно получаться максимальное значение проекции орбитального момента.
\[L={\max \left(M_L\right)\ }=1.\]Основным термом является терм: ${}^3{P,}\ $который состоит из трех состояний: ${}^3{P_{0,1,2}.}$ Основным состоянием является состояние: ${}^3{P_0.}$
Задание: Каким будет эффект Зеемана, если в слабом магнитном поле линии спектра появляются в результате перехода ${}^1P\to {}^1{S\ ?}$
Решение:
Рассмотрим терм вида ${}^1P$. Для данного терма суммарное орбитальное квантовое число равно $1 (L=1)$. Мультиплетность равна:
\[2S+1=1\ \left(2.1\right).\]Следовательно, спиновое квантовое число:
\[S=0.\]Суммарное внутреннее квантовое число $(J)$ при таких условиях равно:
\[J=L=1\left(2.2\right).\]Множитель Ланде при $S=0$ будет: $g_1=1.\ $Магнитное квантовое число будет принимать значения:
\[m_1=-J,\ -J+1,\ \dots ,\ J\left(2.3\right).\]То есть величины
\[m_1=-1,0,1.\]Рассмотрим второй терм: ${}^1{S\ .}\ $Для него $L=0$, мультиплетность:
\[2S+1=1\ \left(2.4\right).\]Следовательно:
\[S=0.\]Получаем, как и в первом случае: $J=L=0$. При $J=0$ расщепления нет. Расщепление по частоте расщепленных уровней запишем как:
\[\triangle \nu =\left(m_1g_1-m_2g_2\right){\nu }_L=m_1\cdot 1\cdot {\nu }_L=m_1{\nu }_L.\]Согласно правилу отбора:
\[m_1-m_2=0,\pm 1.\]Ответ: Эффект Зеемана будет простым, так как линия может расщепляться в данном случае не более, чем на три составляющие.











