Классификация рентгеновских спектров
Рентгеновские спектры возникают при бомбардировке электронами антикатода рентгеновской трубки. Такие спектры делят на два вида: сплошные и линейчатые.
-
Сплошные спектры появляются, когда быстрые электроны тормозятся в веществе антикатода. Это обычное тормозное излучение электронов. Вид данных спектров не зависит от вещества антикатода. Тормозной спектр зависит только от энергии электронов, которые осуществляют бомбардировку антикатода. То, что тормозной спектр является сплошным, согласуется с классической теорией излучения. Но, из классической теории не следует наличие коротковолновой границы сплошного спектра.
-
Если напряжение на рентгеновской трубке повышать, то вместе со сплошным сектором возникает линейчатый спектр. Этот спектр составлен из отдельных линий. Линейчатый спектр зависит от материала антикатода. Элемент имеет свой, характерный только для него, линейчатый спектр, в связи с этим данные спектры носят название характеристических.
Если далее увеличивать напряжение на рентгеновской трубке, то граница коротких волн сплошного спектра перемещается, тогда как, линии характеристического спектра только увеличивают свою интенсивность и при этом их местоположение не изменяется.
Особенности линейчатых рентгеновских спектров
- Рентгеновские линейчатые спектры разных элементов отличаются простотой и однообразием, если их сравнивать с оптическими линейчатыми спектрами. При увеличении номера атома в таблице Менделеева характеристические спектры монотонно смещаются в сторону коротких длин волн.
- Линейчатые рентгеновские спектры различных элементов однотипны, то есть имеют сходный характер, и не изменяются, если изучаемый элемент соединяется с другим элементом. Этот факт объясняют тем, что характеристические спектры рождаются при переходах электронов во внутренних частях атомов. А данные части имеют сходное строение.
- Линейчатые рентгеновские спектры имеют несколько серий, которые называют: $K,L,M,...$ сериями. Каждая серия составлена из небольшого количества линий, например: $K_{\alpha },\ K_{\beta },K_{\gamma },\dots ,L_{\alpha },\ L_{\beta },L_{\gamma },\dots $. При этом длины волн линий убывают.
При анализе рентгеновских линейчатых спектров был сделан вывод о том, что атом имеет систему рентгеновских термов $K,L,M,...\ $(рис.1).
На рис.1 показана схема появления характеристических спектров. Так, возбуждение появляется у атома при удалении одного из внутренних электронов при воздействии электронов или фотонов, которые имеют большую энергию. Если происходит отрывание одного из двух электронов $K$ - уровня $(n-1)$, то вакантное место может заниматься электроном из какого --то уровня находящегося выше ($L,M,...$). Как результат -- возникает K- серия. Аналогично появляются и другие серии: $L,M,...$.
При этом серия $K$ (рис.1) обязательно сопровождается возникновением и остальных серий, так как если происходит испускание ее линий, то освобождаются электроны на уровнях $L,M,...$, они в свою очередь будут заполняться электронами с высших уровней.
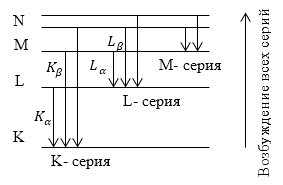
Рисунок 1.
Закон Мозли
Мозли эмпирически установил связь частоты ($\omega $) для $K_{\alpha }$ линии от номера атома элемента в периодической системе. Она имеет вид:
где $R=2,07\cdot {10}^{16}c^{-1}$ -- постоянная Ридберга, $\sigma $ -- постоянная, которая для легких элементов $\sigma \approx 1.$ Для тяжелых элементов $\sigma $ существенно отличается от единицы.
Данный закон имел существенное значение, когда проводилось уточнение месторасположения элементов в системе Менделеева.
Тонкая структура рентгеновских спектров
Точный анализ линейчатых рентгеновских спектров уточнил структуру характеристических термов. Так, $K$ --терм оказался одиночным, $L$- терм тройным, $M$- терм пятикратным.
Отметим, что в данном случае мы имеем дело с $jj$- связью. Данная связь реализуется в глубоких слоях тяжелых атомов.
Для $K$- оболочки мы имеем:
Для $L$- оболочки:
каждый электрон обладает:
В результате получаем три подуровня.
Если по аналогии рассматривать $M$- оболочку, то получится пятикратное расщепление.
Помимо этого, надо учесть, что существуют правила отбора, которым подчиняются переходы между термами ($\triangle l=\pm 1,\ \triangle j=0,\pm 1$). При этом получается, что линии $K$- серии являются дублетами. Составляющие дублетов обозначают индексами ${\alpha }_1,\ {\alpha }_2;;\ {\beta }_1,\ {\beta }_2$. Так, линия $K_{\alpha }$ имеет вид дублета: $K_{{\alpha }_1}\ и\ K_{{\alpha }_2}$. Серии $L$ и выше имеют мультиплетное строение.
Какой будет разность энергий связи электронов $K$ и $L$ оболочек для атома с порядковым номером $Z=23$?
Решение:
Разность энергий связи электронов равна энергии перехода между $L$ и $K$ уровнями и может быть найдена как:
\[\triangle E=\hbar {\omega }_{K_{\alpha }}\left(1.1\right).\]Для нахождения частоты $K_{\alpha }$ -- линии применим закон Мозли:
\[{\omega }_{K_{\alpha }}=\frac{3}{4}R{\left(Z-\sigma \right)}^2\left(1.2\right).\]В результате искомая энергия равна:
\[\triangle E=\hbar \frac{3}{4}R{\left(Z-\sigma \right)}^2\left(1.3\right),\]где для легких элементов $\sigma \approx 1,\ R=2,07\cdot {10}^{16}c^{-1}$. Проведем вычисления:
\[\triangle E=1,05\cdot {10}^{-34}\frac{3}{4}\cdot 2,07\cdot {10}^{16}{\left(23-1\right)}^2=5\ \left(кэВ\right).\]Ответ: $\triangle E=5кэВ\ .$
Как квантовая теория объясняет то, что существует коротковолновая граница сплошного спектра и то, что при увеличении кинетической энергии электронов, которые порождают тормозное излучение, уменьшается длина волны?
Решение:
Предельная энергия кванта соответствует такому варианту торможения, при котором кинетическая энергия электрона полностью переходит в энергию кванте, то есть можно записать:
\[W_{max}=h{\nu }_{max}=q_eU\left(2.1\right),\]где $U$ -- разность потенциалов, которая сообщает электрону энергию $W_{max}.$ ${\nu }_{max}$ -- частота, которая соответствует границе сплошного спектра. Соответственно граничная длина волны (${\lambda }_{min}$) будет равна:
\[{\lambda }_{min}=\frac{c}{{\nu }_{max}}=\frac{ch}{q_eU}=\frac{ch}{W_{max}}\left(2.2\right).\]Ответ: Полученная формула (${\lambda }_{min}=\frac{ch}{W_{max}}$) соответствует экспериментальным данным и дает ответ на вопросы задачи.











