Опыты Резерфорда имеют большое значение в создании представления о том, как устроен атом. Ученый рассматривал рассеяние $\alpha -\ $частиц в веществе. $\alpha $ -- частица -- это частица с положительным зарядом равным 2$\left|q_e\right|$и массой в $7300$ раз большей, чем масса электрона (четыре массы протона). Она состоит из двух протонов и двух нейтронов. Это ядро атома гелия $-4$. Такие частицы появляются при радиоактивных превращениях. Пучки из альфа частиц имеют высокую монохроматичность.
Резерфорд рассматривал прохождение $\alpha $ -- частиц через золотую фольгу толщиной $1$ мкм. Он показал, что основная часть таких частиц испытывает несущественные отклонения, однако отдельные $\alpha $ -- частицы (одна из $20000$) претерпевает резкое отклонение от первоначальной траектории. Порой углы отклонений доходят до $1800$. Электроны, обладая существенно меньшей массой не в состоянии вызвать столь большие изменения направления движения, поэтому Резерфорд сделал вывод, о том, что отклонения $\alpha $ -- частиц вызвано взаимодействием с положительным зарядом большой массы. Но, так как подобные отклонения претерпевают немногочисленные $\alpha $ - частицы, значит, только отдельные экземпляры проходят около положительно заряженной массы, которая сосредоточена в небольшой части объема атома. Для своих опытов Резерфорд использовал $\alpha $- частицы, вылетающие из атомов радиоактивных элементов.
Для анализа рассеяния $\alpha $- частиц можно воспользоваться формулой:
где $d\Omega =2\pi sin\theta d\theta $ -- телесный угол меду косинусами с углами $\theta $ и $d\theta $ (рис.1). $d\sigma =\frac{dN_{\theta }}{N}\ (2)$ -- дифференциальное поперечное сечение упругого рассеяния в угол меду $\theta $ и $d\theta $ (отношение количества частиц рассеянных в угол от $\theta $ до $\theta $+$d\theta $ потоку падающих частиц). $v$ -- скорость рассеиваемой частицы. $m_1$ -- масса точечной движущейся частицы (данная масса много меньше, чем масса частицы, которая электрическое поле создает). Часто в формуле (1) под массой $m_1$ понимают приведенную массу истемы двух частиц, которые взаимодействуют. $Z_1q_e$ -- заряд движущейся частицы, $Z_2q_e$ -- заряд другой точечной частицы, которая создает кулоновское поле. Формула (1) называется формулой Резерфорда. При рассеянии $\alpha $ частиц $Z_1=2.$
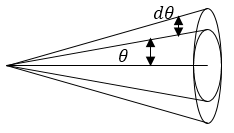
Рисунок 1.
В опытах Резерфорда пучок частиц был направлен на тонкую мишень (во избежание многократных явлений рассеяния толщину мишени стараются сделать как можно тоньше). Получается, что $\alpha $ -- частицы рассеиваются на атомах мишени. Количество $\alpha -$ частиц, которые рассеиваются атомами мишени на разные углы, считают, применяя специальные счетчики.
Выражение (1) при учете формулы (2) позволяет найти количество частиц, которые рассеиваются одним центром. Если число таких центров обозначит как n, то количество рассеянных в телесный угол $d\Omega $ частиц равно:
где $Zq_e$ -- заряд рассеивающего атома. Если $d\Omega =const$, то получим:
В опытах Резерфорда в первую очередь проверялось выполнение условия (4). Оно выполнялось с большой точностью. Что свидетельствует о том, что формула (3) является верной и роль многократного рассеяния не играет существенной роли.
Вычисление заряда ядра -- первый результат из опытов Резерфорда
Все параметры, входящие в формулу (3) либо известны, либо могут быть измерены экспериментально. Исключение составляет $Z$. Значит, данная формула дает возможность определить $Z$ для атомов вещества, которое осуществляет рассеивание. Кроме того, оказалось, что $Z$ совпал с порядковым номером элемента в периодической системе. Что указала на то, что в системе Менделеева элементы расположены по возрастанию заряда $Zq_e$. Это один из самых значимых выводов из опытов Резерфорда.
Распределение заряда в атоме -- второй вывод из опытов Резерфорда
Многие из отклоненных $\alpha -$ частиц изменяют свое направление движения на углы $\theta =\frac{\pi }{2}$ и больше. Подобные углы отклонения становятся возможными, если положительных заряд ядра атома распределен в объеме много меньшем, чем прицельное расстояние, которое измерялось в эксперименте. Зная кинетическую энергию $\alpha -$ частиц и прицельное расстояние, вычислялись линейные размеры атома. Он получались порядка (${10}^{-10}м$). Если представить, что положительный заряд атома распределен равномерно по такому объему, то рассеяние на большие углы не получится. Отсюда делался вывод о том, что в атоме положительный заряд занимает малую часть объема атома (область порядка ${10}^{-15}м$). Данная область носит название ядра атома.
Вокруг ядра движутся электроны. Так как размеры атома порядка ${10}^{-10}м$, делают вывод, что расстояние от электронов до ядра имеет тот же порядок (${10}^{-10}м$). Масса электронов мала в сравнении с массой атома, считается, что ядро -- сосредотачивает основную долю массы. Так, опыты Резерфорда подтверждают его планетарную модель атома.
Задание: Тяжелое ядро свинца покоится. Определите, на какое минимальное расстояние может приблизиться $\alpha $ частица, которая имеет кинетическую энергию равную $E_k=0,2\ Mэв$? Соударение считать лобовым.
Решение:
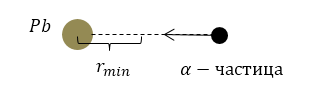
Рисунок 2.
Рассматриваем частицы как точечные, запишем закон сохранения энергии в виде:
\[E_k=E_p\left(1.1\right),\]где в левой части имеется кинетическая энергия движущейся (до столкновения) $\alpha $ -- частицы. Эта энергия переходит в потенциальную энергию взаимодействия ядра свинца и $\alpha $ -- частицы. Выражение для $E_p$ можно представить как:
\[E_p=\frac{q_{pb}q_{\alpha }}{{4\pi {\varepsilon }_0r}_{min}}\ \left(1.2\right),\]где $q_{pb}=Zq_e$, $Z$- число протонов, $q_{\alpha }=2q_e$. Подставим заряды ядер, выразим искомое расстояние, имеем:
\[r_{min}=\frac{Zq_e2q_e}{4\pi {\varepsilon }_0E_k}.\]Из таблицы Менделеева найдем, что для свинца $Z=82$, ${\varepsilon }_0=8,85\cdot {10}^{-12}\frac{Ф}{м}$, $E_k=0,2\ Mэв=0,2\cdot {10}^6\cdot 1,6\cdot {10}^{-19}Дж$. $q_e=1,6 \cdot {10}^{-19}Кл.$
Проведем расчет:
\[r_{min}=\frac{82\cdot {(1,6\cdot {10}^{-19})}^2\cdot 2}{4\pi \cdot 8,85\cdot {10}^{-12}\cdot 0,2\cdot {10}^6\cdot 1,6\cdot {10}^{-19}}=\frac{82\cdot 4\cdot {10}^{-19}}{\pi \cdot 8,85\cdot {10}^{-12}}=\frac{328\cdot {10}^{-19}}{27,79\cdot {10}^{-6}}\approx 1,18\cdot {10}^{-12}\left(м\right).\]Ответ: $r_{min}=1,18\cdot {10}^{-12}$пм.
Задание: Как объясняются результаты опытов Резерфорда с точки зрения ядерной модели атома?
Решение:
Опыты Резерфорда показали, что в большинстве случаев $\alpha $ -- частицы после того, как прошли сквозь фольгу не изменяют направления своего движения или отклоняются на малые углы. Небольшая часть $\alpha $ -- частиц терпят отклонения на большие углы (порядка $1350 - 1500$). Объяснить такие большие углы накоплением небольших отклонений не представляется возможным.
Результаты опытов Резерфорда получают понятное объяснение из ядерной модели атома. Тогда, кода $\alpha $ -- частица проходит сквозь электронную оболочку атома она не испытывает существенного отклонения от первоначального направления движения. Так как электроны обладают малой массой, и их заряд распределён по всему объему оболочки. Те $\alpha $ -- частицы, которые пролетают около ядра, испытывают большие отклонения. При малых расстояниях силы отталкивания между $\alpha $ -- частицей, обладающей положительным зарядом и положительно заряженным ядром с существенной массой достаточно велики. Это вызывает существенное отклонение $\alpha $ -- частиц, от первоначального направления движения. Вероятность непосредственного попадания $\alpha $ -- частицы в ядро малое по объему мала. Значит, количество $\alpha $ -- частиц, претерпевших большое отклонение, будет малым.












