Явление электронного парамагнитного резонанса
Если парамагнитный атом поместить в магнитное поле, то каждый его энергоуровень будет расщепляться на количество подуровней равных $2J+1$(количество возможных $m_J)$. Интервал между соседними уровнями при этом равен:
В том случае, если атом в данном состоянии поместить еще в электромагнитную волну, имеющую частоту $\omega $, которая удовлетворит условию:
то под воздействием магнитной компоненты волны в соответствии с правилом отбора будут возникать переходы атома между соседними подуровнями, внутри одного уровня. Такое явление называют электронным парамагнитным резонансом (ЭПР). Первым его отметил Е.К. Завойский в 1944 г. Так как ЭПР связано с резонансом, то переходы появляются только при определенной частоте падающей волны. Такую частоту легко оценить, если использовать выражение (2):
При $g\approx 1$ и типичной индукции магнитного поля, которое используют в условиях лаборатории, $B\approx 1\ Тл$ получают $\nu ={10}^{10}Гц$. Что означает, что частоты локализованы в радиодиапазоне (СВЧ).
При явлении резонанса энергия передается от поля к атому. Кроме того, при переходе атома с высоких подуровней Зеемана на более низкие подуровни, энергия передается от атома к полю. Надо отметить, что в случае теплового равновесия количество атомов имеющих меньшую энергию больше, чем число атомов обладающих большей энергией. Значит, переходы, которые увеличивают энергию атомов, превалируют над переходами в сторону с меньшей энергией. Получается, что парамагнетик поглощает энергию поля в радиодиапазоне и при этом увеличивает свою температуру.
Опыты с явлением электронного парамагнитного резонанса дали возможность, применяя выражение (2), находить один из параметров: $g,B\ или\ {\omega }_{rez}$ по остальным величинам. Так, измеряя с высокой точностью $B$ и ${\omega }_{rez}$ в состоянии резонанса, находят величину фактора Ланде и магнитный момент атома в состоянии с J.
В жидкостях и твердых телах атомы нельзя считать изолированными. Пренебрегать их взаимодействием нельзя. Оно ведет к тому, что интервалы между соседними подуровнями при расщеплении Зеемана являются разными, линии ЭПР имеют конечную ширину.
ЭПР
Итак, явление электронного парамагнитного резонанса состоит в поглощении парамагнетиком микроволнового радиоизлучения за счет переходов между подуровнями расщепления Зеемана. При этом расщепление энергоуровней вызвано воздействием постоянного магнитного поля на магнитные моменты атомов вещества. Магнитные моменты атомов в таком поле ориентируются по полю. Одновременно с эти идет расщепление энергоуровней Зеемана и перераспределение по данным уровням атомов. Заполняемость атомами подуровней оказывается разной.
В состоянии термодинамического равновесия среднее количество атомов ($\left\langle N\right\rangle $), заселяющих данный подуровень можно вычислить, используя формулу Больцмана:
где $\triangle E_{mag}\sim mH$. Подуровни с меньшим магнитным квантовым числом ($m$) имеют больше атомов, как состояния с меньшей потенциальной энергией. Значит, существует преимущественная ориентация магнитных моментов атомов по магнитному полю, которая соответствует намагниченному состоянию парамагнетика. В случае накладывания на парамагнетик переменного магнитного поля с частотой равной (кратной) частоте перехода между подуровнями расщепления Зеемана происходит резонансное поглощение электромагнитных волн. Оно вызвано превышением количества переходов, которые связаны с увеличением магнитного квантового числа на один:
над количеством переходов типа:
Так, из-за резонансного поглощения энергии переменного магнитного поля атомы будут совершать переходы с нижних более заполненных уровней, на верхние уровни. Поглощение пропорционально количеству поглощающих атомов в единице объема.
Если вещество составлено из атомов с одним валентным электроном в состоянии s, имеющих полный магнитный момент равный спиновому магнитному моменту s - электрона, то ЭПР наиболее эффективен.
Особенным парамагнитным резонансом считают резонансное поглощение электромагнитных волн электронами проводимости в металлах. Оно связано со спином электронов и спиновым парамагнетизмом электронного газа в таком веществе. В ферромагнетиках выделяют ферромагнитный резонанс, который связывают с переориентацией электронных моментов в доменах или между ними.
Для изучения электронного парамагнитного резонанса используют радиоспектроскопы. В таких приборах частота ($\omega $) остается неизменной. Изменяют индукцию магнитного поля (B), которое создает электромагнит (рис.1).
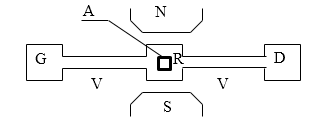
Рисунок 1. Электронный парамагнитный резонанс (ЭПР). Автор24 — интернет-биржа студенческих работ
Маленький образец А располагают в объемном резонаторе R, который настроен на длину волны около 3 см. Радиоволны такой длины создаются генератором G. Эти волны через волновод V подводят к резонатору. Часть волн поглощается образцом А, часть из них через волновод попадают в детектор D. При проведении опыта проводят плавное изменение индукции магнитного поля (B), которое создается электромагнитом. Когда величина индукции удовлетворяет условию возникновения резонанса (2) образец начинает интенсивно поглощать волну.
ЭПР один из самых простых методов радиоспектроскопии.
Примеры
Задание: Каков магнитный момент атома $Ni$ в состоянии ${{}^3F}_4$, если резонансное поглощение энергии возникает при воздействии постоянного поля с магнитной индукцией $B_0$ и переменного магнитного поля с индукцией $B_0$, перпендикулярного к постоянному полю. Частота переменного поля равна $\nu $.
Решение:
Как известно в состоянии резонанса выполняется равенство:
\[\hbar \omega =h\nu =\delta E={\mu }_bgB\left(1.1\right).\]Из формулы (1.1) найдем фактор Ланде:
\[g=\frac{h\nu }{{\mu }_bB_0,\ }.\]Для заданного состояния (${{}^3F}_4$) имеем: $L=3$, $S=1$, $J=4$. Магнитный момент задан при помощи выражения:
\[\mu ={\mu }_bg\sqrt{J(J+1)}=\frac{h\nu }{B_0,\ }\sqrt{20}.\]Ответ: $\mu =\frac{h\nu }{B_0,\ }\sqrt{20}.$
Задание: Какую полезную информацию можно получить при изучении электронного парамагнитного резонанса?
Решение:
Эмпирически получив резонанс из условий резонанса можно найти одну из величин: фактор Ланде ($g$), индукцию магнитного поля в условиях резонансного поглощения энергии атомом (B), резонансную частоту (${\omega }_{rez}$). При этом B и ${\omega }_{rez}$ можно измерить с высокой точностью. Следовательно, ЭПР дает возможность получить значение $g\ $с высокой точностью и, следовательно, магнитный момент атома для состояния с квантовым числом $J$. Величина квантового числа S определяется по мультиплетности спектров. Если известны $g,\ J,\ S$ легко вычислить $L$. Получается, что становятся известными все квантовые числа атома и спиновый орбитальный и полный магнитный моменты атома.











