Электронная конфигурация
Состояние изолированного электрона в поле сил Кулона определяют, используя четыре квантовых числа:
- главное квантовое число $n=1,2,3,\dots $
- орбитальное квантовое число $l=0,1,2,3,\dots n-1.$
- магнитное квантовое число $m_l=-l,-l+1,\dots ,\ l-1,l.\ $
- спином $m_s=\pm \frac{1}{2}$.
Для первого приближения при характеристике состояния электрона в атоме применяют эти же квантовые числа, даже если учитывают взаимодействия между электронами.
Система из электронов в атоме, которые имеют одинаковые числа $n$ образуют оболочку атома. Оболочки обозначают буквенными символами (табл.1).

Рисунок 1.
Движение электрона по орбите обозначают буквами в соответствии с табл.2
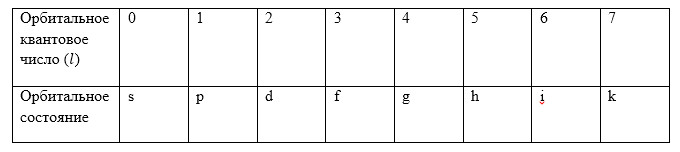
Рисунок 2.
Электронную структуру записывают так: число, находящееся слева -- главное квантовое число $(n)$, сам спектроскопический символ соответствует величине орбитального квантового числа ($l$).
Полное описание состояния атома требует вместе с указанием полных $L,S,J$ перечисления всех состояний электронов. Так, например, запись: $1s2p^3P_0$ обозначает состояние атома гелия, имеющего $L=1,S=1,J=0$ и два электрона в состояниях $1s$ и $2p$. В том случае, если несколько электронов находятся в состояниях с одинаковыми $n\ и\ l\ $, то данный факт обозначают как степень. $2p^3$ - три электрона в состоянии $2p$.
О распределении электронов в атоме по состояниям с разными $n\ и\ l$ говорят как об электронной конфигурации.
При известных $n\ и\ l$ электрон может иметь разные значения проекций орбитального момента ($m_l$) и спина ($m_s$) на ось $Z$.
В качестве основания для строения электронных оболочек атомов используют:
-
Принцип Паули: Атому не может принадлежать два электрона, которые бы характеризовались одинаковыми четверками квантовых чисел.
-
Принцип минимума энергии: при известном суммарном числе электронов в атоме реализуется состояние с минимальной энергией. Принцип минимума энергии коррелирует с условием устойчивости атома.
Общее правило, которое описывает порядок заполнения электронных состояний -- это правило Клечевского: В атоме со многими электронами первыми заполняются состояния с минимально возможной суммой ($n+l$), а для равных величин $(n+l$) состояния с минимальным $n$.
Электронную структуру атома записывают в виде электронной конфигурации с указанием числа электронов на каждой орбитали.
Иерархия взаимодействий в многоэлектронном атоме
В атоме с несколькими электронами выделяют $4$ основных вида взаимодействий. В зависимости от них применяется система классификации электронных состояний атома.
-
Взаимодействие электронов с ядром при помощи сил Кулона.
-
Меж электронное электростатическое взаимодействие.
-
Спин -- орбитальное взаимодействие.
-
Взаимодействие электронов с внешним полем.
Для атома в нормальном состоянии самым сильным является взаимодействие электронов с ядром, оно является определяющим для существования атома или иона. Данное взаимодействие ответственно за грубое деление состояний электрона по уровням энергии, благодаря чему появляется возможность использования электронной конфигурации атомов.
Взаимодействие между электронами и спин-орбитальное взаимодействия являются более «тонкими». Эти взаимодействия определяют применяемую классификацию электронного состояния атома. Если учитывать только меж электронное взаимодействие и не учитывать спин -- орбитальное взаимодействие (при $E_{ee}\gg E_{LS\ \ },$ где $E_{ee}-\ $энергия взаимодействия электронов между собой, $E_{LS\ \ }\ $- энергия спин -- орбитального взаимодействия) (при этом вводят термы в которых величины квадратов орбитального и спинового моментов суммы электронов в атоме определяются точно), то такая схема построения термов называется $LS$ -- приближением (приближением Рассела - Саундерса). Данная схема реализуется не всегда. В приближении $LS$ связи понятия: конфигурация электронов -- терм -- состояние отражает иерархию взаимодействий в атоме: взаимодействие электронов с ядром -- электростатическое взаимодействие электронов -- спин-орбитальное взаимодействие. Как результат: взаимодействие электронов ведет к групповым состояниям электронной оболочки, при этом имеется определенное значение полного орбитального момента электронов $(L)$. В таком случае спины электронов не задействованы, и они складываются (независимо) в полный спин $S$. В случае необходимости далее учитывается спин-орбитальное взаимодействие, которое связывает полный орбитальный момент и полный спин и ведет к дополнительному расщеплению групповых состояний электронов по величине полного момента $J$.
Эмпирически показано, то приближение $LS$-связи хорошо применимо для несильно возбужденных состояний и не тяжелых атомов (до $Fe$). Термы при этом имеют обозначения: ${}^{2S+1}{L_J.}$
В случае, если энергия спин --орбитального взаимодействия много больше, чем энергия электростатического взаимодействия электронов ($E_{LS}\gg E_{ee}$), то электростатическим взаимодействием электронов в атоме можно пренебречь. В таком случае состояние каждого электрона определяют квантовыми числами ($j$, $m_j$). Если известны значения $j$ для всех электронов атома в известной конфигурации ($j=1,...N$), то считают, что известен терм атома в приближении $jj$ --связи. Такой терм обозначают как:
Если в дальнейшем учитывают электростатическое взаимодействие электронов, то терм расщепляется на группу состояний, количество которых определено числом значений $J$ (возможные значения полного механического момента атомарной электронной оболочки):
При $jj$ -- взаимодействии последовательность интенсивности взаимодействия следующая: взаимодействие электронов и ядра -- спин -- орбитальное взаимодействие -- электростатическое взаимодействие.
Задание: Рассмотрите в рамках $LS$ -- связи предельные случаи наложения внешнего магнитного поля.
Решение:
Пусть энергия взаимодействия электронов с внешним магнитным полем ($E_H$) много меньше энергии спин -- орбитального взаимодействия ($E_{LS}$), (то есть $E_{LS}\gg E_H$). В таком случае говорят о эффекте Зеемана. Внешнее магнитное поле взаимодействует с полным магнитным моментом атома (J) при этом, оно расщепляет состояние по величине проекции $J_z\ $ на $2J+1$ составляющих.
Допустим, что энергия взаимодействия электронов с внешним магнитным полем ($E_H$) много больше энергии спин -- орбитального взаимодействия ($E_{LS}$), (то есть $E_H\gg E_{LS}$). В данном случае возникает эффект Пашена -- Бака. При этом считают, что внешнее магнитное поле сильно на столько, что оно разрывает связь орбитального момента и спина. Расщепление при этом происходит по параметру ($2L_z+S_z$).
В большом числе случаев, если внешнее поле составляет несколько Тесла, то проявляется эффект Зеемана, но так как параметры спин-орбитального взаимодействия атомов существенно отличаются, для легких атомов (например $Li$) в поле порядка $3$ Тл появляются спектры относящиеся к эффекту Пашена - Бака.
Задание: Составьте электронные конфигурации элементов от $H$ до $Ne$ периодической системы элементов и $K$.
Решение:
В начале периодической системы, когда количество электронов мало, роль их взаимодействия не является существенной. Заполнение электронных состояний идет по идеальной схеме. Так, водород имеет один электрон, его состояние имеет минимальную энергию ($n=1$), электронная конфигурация водорода: $1s.$
Следующий элемент таблицы Менделеева - гелий ($He$) имеет два электрона. Электроны находятся в состоянии $1s$, но имеют противоположные спины. Электронная конфигурация $He:$ $1s^2$. Это так называемый парагелий. У ортогелия спин второго электрона совпал по направлению с первым электроном и он не может находиться в состоянии $1s$. Ближайшее допускаемое по состояние электрона при этом будет $2s$. Электронная конфигурация ортогелия запишется как: $1s2s.$ Инертный газ гелий заканчивает заполнение первой оболочки и он является последним в первом периоде элементов системы.
В литии ($Li$) заполняется вторая оболочка. В электронной конфигурации парагелия добавляется один электрон. Электрон добавляется в $2s$ -- состояние, так как третьего электрона в $1s$ состоянии быть не может в соответствии с принципом Паули. Электронная конфигурация лития: $1s^22s.\ $ Следующий элемент периодической системы -- бериллий ($Be$): $1s^22s^2$. Далее идет Бор (B): $1s^22s^22p.$ В $p$ -- состоянии может пребывать $6$ электронов $(2(2+1)=6)$. При последовательном переходе от бора до неона включительно заполняются оболочки элементов $2p$ -- состояния. При этом имеем электронные конфигурации:
\[C:\ 1s^22s^22p^2,\ N:1s^22s^22p^3,\ O:1s^22s^22p^4,\ F:1s^22s^22p^5,\ Ne::1s^22s^22p^6.\]Инертным неоном завершается заполнение второй $L$- оболочки и второго периода.
В соответствии с идеальной схемой заполнения конфигурация $K$ должна быть: $1s^22s^22p^63s^23p^63d$, но на самом деле это не так. С точки зрения энергии боле выгодным является состояние $4s$, а не $3d$. Этот факт подтвержден прямыми расчетами и экспериментально. Конфигурация калия имеет вид:
\[K:1s^22s^22p^63s^23p^64s.\]










