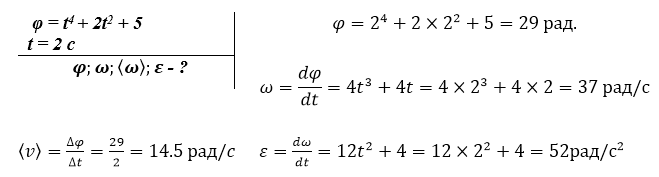Существует пять видов движения твердого тела:
- поступательное движение;
- вращение вокруг неподвижной оси;
- плоское движение;
- вращение вокруг неподвижной точки;
- свободное движение.
Первые два называются простейшими движениями твердого тела. Остальные виды движений можно представить как комбинацию основных движений.
Поступательным называется такое движение твердого тела, при котором любая прямая, проведенная в этом теле, перемещается, оставаясь параллельной своему начальному направлению.
Любое прямолинейное движение является поступательным. Однако поступательное движение не следует смешивать с прямолинейным. При поступательном движении тела траектории его точек могут быть любыми кривыми линиями.
Рис.1 Поступательное криволинейное движение кабин колеса обзора
Свойства поступательного движения определяются следующей теоремой: при поступательном движении все точки тела описывают одинаковые (при наложении совпадающие) траектории и имеют в каждый момент времени одинаковые по модулю и направлению скорости и ускорения.
Из теоремы следует, что поступательное движение твердого тела определяется движением какой-нибудь одной из его точки. Следовательно, изучение поступательного движения тела сводится к задаче кинематике точки.
При поступательном движении общую для всех точек тела скорость $\overrightarrow {v}$ называют скоростью поступательного движения тела, а ускорение $\overrightarrow {a}$ - ускорением поступательного движения тела. Векторы $\overrightarrow {v}$ и $\overrightarrow {a}$ можно изображать приложенными в любой точке тела.
Заметим, что понятие о скорости и ускорении тела имеют смысл только при поступательном движении. Во всех остальных случаях точки тела, движутся с разными скоростями и ускорениями, и термины «скорость тела» или «ускорение тела» для этих движений теряют смысл.
Вращательным движением абсолютно твердого тела вокруг неподвижной оси называется такое его движение, при котором все точки тела движутся в плоскостях, перпендикулярных к неподвижной прямой, называемой осью вращения, и описывают окружности, центры которых лежат на этой оси.
Для определения положения вращающегося тела проведем через ось вращения, вдоль которой направим ось Az, полуплоскость - неподвижную и полуплоскость, врезанную в само тело и вращающуюся вместе с ним (рис. 2).
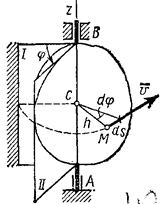
Рисунок 2. Угол поворота тела
Тогда положение тела в любой момент времени однозначно определится взятым с соответствующим знаком углом $\varphi $ между этими полуплоскостями, который назовем углом поворота тела. Будем считать угол $\varphi $ положительным, если он отложен от неподвижной плоскости в направлении против хода часовой стрелки (для наблюдателя, смотрящего с положительного конца оси Az), и отрицательным, если по ходу часовой стрелки. Измерять угол $\varphi $ будем всегда в радианах. Чтобы знать положение тела в любой момент времени, надо знать зависимость угла $\varphi $ от времени t, т.е. ${\mathbf \varphi }$=f(t). Это уравнение выражает закон вращательного движения твердого тела вокруг неподвижной оси.
При вращательном движении абсолютно твердого тела вокруг неподвижной оси углы поворота радиуса-вектора различных точек тела одинаковы.
Основными кинематическими характеристиками вращательного движения твердого тела являются его угловая скорость $\omega $ и угловое ускорение $\varepsilon $.
Уравнения, описывающие вращательное движение, можно получить из уравнений поступательного движения, произведя в последних следующие замены: перемещение s --- угловое перемещение (угол поворота) $\varphi $, скорость u --- угловая скорость $\omega $, ускорение a --- угловое ускорение $\varepsilon $.

Материальная точка движется по прямой. Уравнение ее движения $s = t^4 + 2t^2 + 5$. Определить мгновенную скорость и ускорение точки в конце второй секунды от начала движения, среднюю скорость и путь, пройденный за это время.
Решение
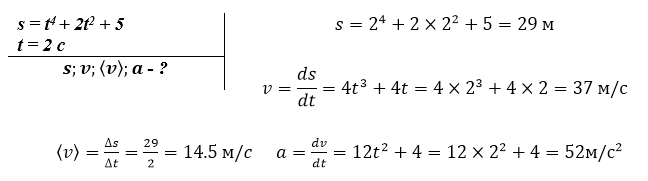
Тело вращается вокруг неподвижной оси. Уравнение его движения ${\mathbf \varphi }$ = $t^4 + 2t^2 + 5$. Определить мгновенную угловую скорость и угловое ускорение тела в конце второй секунды от начала движения, среднюю угловую скорость и угол поворота за это время.
Решение