Разветвленные цепи
На практике цепи могут быть очень сложными, могут состоять из нескольких источников тока, большого количества сопротивлений. Однако в цепь любой сложности входят два вида простых элементов:
- узлов -- точек цепи, в которых встречаются более чем два проводника с током (рис.1) (Например, точки С и D);
- замкнутых контуров (рис. 1) (ABDCA, CDFEC, ABFEA).
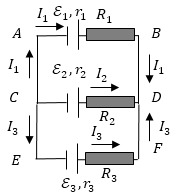
Рис. 1
Правила Кирхгофа
Правила Кирхгофа используют для создания системы уравнений, из которой находят силы тока для цепи любой сложности. По своей сути они -- законы Ома для каждого из контуров и законы сохранения заряда в каждом узле.
Первое правило Кирхгофа (правило узлов): Сумма алгебраических значений токов ${(I}_l)$ сходящихся в каждом узле, равна нулю:
где n- количество проводников, сходящихся в узле. Надо отметить, что положительными обычно принимают токи, которые к узлу подходят.
Правило Кирхгофа номер два: (правило контуров): Сумма произведений на сопротивления соответствующих участков каждого из замкнутых контуров равна сумме алгебраических значений сторонних ЭДС ($\mathcal E$) в каждом замкнутом контуре:
В случае, когда используют правило Кирхгофа номер 2 задают направление обхода контура. Токи ${(I}_l)$, которые совпали по направлению с направлением обхода, полагают большими нуля. ЭДС ${(\mathcal E}_i)$ считают положительными, в том случае если они создают токи, которые направлены в сторону заданного обхода контура.
Система уравнений, которая получается в результате использования правил Кирхгофа, является полной и позволяет вычислять все токи в системе.
Таким образом, применения правил Кирхгофа следующий:
- произвольным образом выбираем для всех участков цепи направления токов;
- для $m$ узлов цепи записываем $m-1$ независимых уравнений первого правила Кирхгофа для токов;
- последовательно выделяем произвольные замкнутые контуры, которые содержат не меньше одного участка цепи, не входящего в предыдущие контуры. В разветвленной цепи, которая состоит из $n$ ветвей и $m\ $узлов, количество независимых уравнений, записанных с использованием второго правила Кирхгофа равно $n-m+1$.
Итак, если выписывать все уравнения по правилам Кирхгофа для всех контуров и всех узлов, то получится уравнений больше, чем необходимо, так как не все уравнения независимы. Чтобы не усложнять себе работы и не выписывать лишних уравнений, надо руководствоваться следующими правилами: записывая очередное уравнение для замкнутых контуров, надо следить, чтобы оно имело хотя бы одну величину, которая раньше в уравнения не входила, если все величины в уравнениях уже были, такое уравнение лишнее. Аналогично делают при выписывании уравнений для узлов. Затем, контроль правильности в написании уравнений состоит в проверке полноты системы уравнений. Количество уравнений должно быть равно числу неизвестных.
Задание: В электрической схеме, приведенной на рис. 2, заданы $R_2,\ R_3,\ R_4$ и ЭДС: $\mathcal E_1,\ \mathcal E_2$. Требуется определить $R_1$, при условии, что ток в цепи гальванометра G отсутствует ($I_G=0)$.
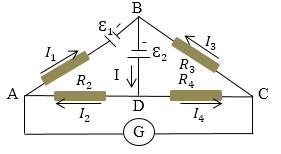
Рис. 2
Зададим направления токов рис. 2, тогда для узлов A,B,C первое правило Кирхгофа записывается в виде:
\[I_2-I_1=0\left(1.1\right).\] \[I_1+I_3=I(1.2),\] \[I_4-I_3=0\left(1.3\right).\]За направление обхода контура примем движение против часовой стрелки, получим:
\[{Для\ контура\ ABCGA:\ -I}_1R_1+I_3R_3=\mathcal E_1(1.4)\] \[{Для\ контура\ ADCGA\ I}_2R_2-I_4R_4=0(1.5),\] \[{Для\ контура\ BCDB:\ I}_3R_3+I_4R_4=\mathcal E_2(1.6)\]Решаем систему уравнений (1.1)-(1.6)и имеем:
\[R_1=\frac{R_3R_2}{R_4}-\frac{R_2\left(R_3+R_4\right)}{R_4}\cdot \frac{\mathcal E_1}{\mathcal E_2}.\]При $\mathcal E_1=0$ результат не зависит от $ЭДС$, получаем схему мостика Уитстона для измерения сопротивлений:
Ответ: Искомое $R_1$ в заданной схеме можно найти в соответствии с формулой: $R_1=\frac{R_3R_2}{R_4}-\frac{R_2(R_3+R_4)}{R_4}\cdot \frac{\mathcal E_1}{\mathcal E_2}$.
Задание: $R_1,R_2,R_3$, а также источник тока с ЭДС равным $\mathcal E_1$ соединены как показано на рис.3. Определите ЭДС источника тока, который надо подключить в цепь между точками А и В, чтобы через $R_3$ шел ток I в направлении, которое указано стрелкой. Сопротивлением источника пренебречь.
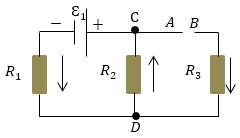
Рис. 3
Решение:
За основу решения примем законы Кирхгофа одно для токов (2.1):
\[I_1-I_2+I=0\ \left(2.1\right).\]Выберем направление обхода -- против часовой стрелки. Запишем два уравнения, используя второе правило Кирхгофа:
\[I_1R_1+I_2R_2=-_1\left(2.2\right).\] \[{-I}_2R_2-IR_3=\mathcal E \left(2.3\right).\]Из уравнения (2.1) выразим $I_1$, получим:
\[I_1=I_2-I\ \left(2.4\right).\]Подставим в (2.2), получим:
\[\left(I_2-I\right)R_1+I_2R_2=-\mathcal E_1\to I_2=\frac{IR_1-\mathcal E_1}{R_1+R_2}\left(2.5\right).\]Подставим $I_2$ из (2.5) в (2.3) получим искомую ЭДС:
\[-\frac{IR_1-\mathcal E_1}{R_1+R_2}R_2-IR_3=\mathcal E\]Ответ: $\mathcal E=-\frac{IR_1-\mathcal E_1}{R_1+R_2}R_2-IR_3$ у ЭДС источника в точке A -- минус, в точке В -- плюс.












