Определение для напряжения в проводнике с током
В том случае если в проводнике есть эклектический ток, значит между любыми двумя его точками, есть разность потенциалов (${\varphi }_1-{\varphi }_2$), которая в электростатике совпадает с напряжением (U). Мы записывали, что:
Однако, для существования постоянного тока в проводнике по мимо кулоновских должны присутствовать сторонние силы, напряженность в данной точке поля в проводнике с током равна:
где $\overrightarrow{E}$ напряженность электрического поля, которая является суммой напряжённости кулоновского поля (${\overrightarrow{E}}_q$) и поля сторонних сил (${\overrightarrow{E}}_{stor}$). Следовательно, напряжение в проводнике с током не будет совпадать с разностью потенциалов.
Напряжением (падением напряжения) $U_{21}$ на участке цепи 1-2 по которому идет ток называется величина, которая равна работе, совершаемой кулоновскими и сторонними силами при перемещении единичного положительного заряда на данном участке:
где $d\overrightarrow{l}$-вектор, численно равный элементу длины проводника и направленный по касательной к проводнику, совпадающий по направлению с вектором плотности тока.
Если подставить в (4) уравнение (2), то мы получим:
где ${{\mathcal E}}_{stor}$ -- электродвижущая сила на участке цепи 1-2, равная:
${\varphi }_1-{\varphi }_2$ -- разность потенциалов электростатического поля в точках 1 и 2, которая равна:
Очевидно, что если цепь замкнута, то
В таком случае для замкнутой цепи, мы получим:
Основной единицей измерения напряжения в системе СИ является вольт -- В.
Связь силы тока и напряжения для участка цепи
Такая физическая величина, как напряжение, фигурирует во многих законах относящихся к электродинамике. Так, одним из немаловажных законов является закон Ома для произвольного участка цепи, который записывается как:
Формула (7) показывает, что напряжение на участке 1-2 равно произведению силы тока, который течет через этот участок на сопротивление этого участка. Часто индексы, которые стоят в формуле (7) у напряжения и сопротивления опускают.
Виды напряжения
На практике выделяют: мгновенное напряжение, амплитудное напряжение, среднее значение напряжения, среднеквадратичное напряжение, средневыпрямленное напряжение.
- Мгновенное напряжение ($U_m$) -- равно разности потенциалов двух точек проводника с током в заданный момент времени. Данное напряжение является функцией от времени.
- Амплитудное напряжение ($U_{max}$) -- максимальное значение (по модулю) мгновенного напряжения за период изменений напряжения.
- Среднее значение напряжения за период колебаний (T) находят как: \[\left\langle U\right\rangle =\frac{1}{T}\int\limits^T_0{U\left(t\right)dt\left(11\right).}\]
- Среднеквадратичное напряжение вычисляется в соответствии с формулой: \[U_{kv}=\sqrt{\frac{1}{T}\int\limits^T_0{U^2\left(t\right)dt}}\left(12\right).\]
- Средневыпрямленное напряжение ($U_v$) определено как: \[U_v=\frac{1}{T}\int\limits^T_0{\left|U(t)\right|}dt\ \left(14\right).\]
Для гармонически изменяющегося напряжения выполняется равенство:
\[U_{kv}=\frac{1}{\sqrt{2}}U_{max}\left(13\right).\]Для гармонически изменяющегося напряжения выполняется равенство:
\[U_v=\frac{2}{\pi }U_{max}\left(15\right).\]Напряжение при соединении проводников
При последовательном соединении проводников (рис.1), суммарное напряжение в цепи находится как сумма напряжений:

Рис. 1
При параллельном соединении (рис.2) результирующее напряжение постоянно. Сила тока равна сумме токов в проводниках:
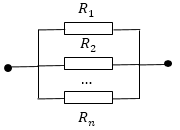
Рис. 2
Задание: На рис.3 изображена замкнутая цепь, которая содержит сопротивление и источник тока ЭДС которого равна $\mathcal E$, внутреннее сопротивление источника r.
Найдите напряжение на внешней цепи, зная параметры источника тока и силу тока в цепи I.
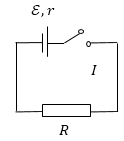
Рис. 3
Решение:
Если цепь замкнута, то ${\varphi }_1={\varphi }_2$. Напряжение на клеммах источника тока (на внешней цепи) равно:
\[{\mathcal E}=IR\ \left(1.1\right),\]где ${\mathcal E}$ - алгебраическая сумма всех ЭДС в цепи.
Напряжение на внешней цепи, которая задана, равно:
\[U=IR_1(1.2)\]Если источник ЭДС имеет внутреннее сопротивление r, то для сопротивления всей цепи (R) запишем:
\[R=R_1+r\to R_1=R-r\ \left(1.3\right),\]где $r$ -- внутреннее сопротивление источника.
Cила тока во внешней цепи, равна:
\[I=\frac{{\mathcal E}}{R_1+r}\left(1.4\right).\]Подставим в (1.1) формулы (1.4) и (1.3), получим:
\[U=\frac{{\mathcal E}R_1}{R_1+r}=\frac{{\mathcal E}\left(R-r\ \right)}{R_1+r}=\frac{{\mathcal E}R}{R_1+r}-\frac{{\mathcal E}r}{R_1+r}=IR-Ir={\mathcal E}-Ir.\]Ответ: $U={\mathcal E}-Ir.$
Задание: Как можно измерить ЭДС источника тока?
Решение:
При разомкнутой цепи сила тока в ней равна нулю (I=0), Исходя из результата предыдущего примера в цепи (рис. 3) мы имеем:
\[U={\mathcal E}-Ir\ \left(2.1\right)\]при I=0 из (2.1) получаем, что:
\[U={\mathcal E}\left(2.2\right).\]А так как сторонние силы при разомкнутой цепи работы не совершают, то:
\[U={\varphi }_1-{\varphi }_2(2.3).\]Следовательно, можно записать, что при разомкнутой цепи:
\[{\mathcal E}={\varphi }_1-{\varphi }_2.\]Ответ: Для того чтобы найти ${\mathcal E}$ источника тока можно измерить разность потенциалов на его клеммах в ситуации, когда цепь не замкнута.












