Определение
Потоком вектора магнитной индукции (магнитным потоком) (Ф) через площадку S называют скалярную величину равную:
\[Ф=BScos\alpha ={\ B}_nS=\overrightarrow{B}\overrightarrow{S}\left(1\right),\]где $\alpha $ угол между $\overrightarrow{n}$ и $\overrightarrow{B}$, $\overrightarrow{n}$ -- нормаль к площадке S.
Ф равен количеству линий магнитной индукции, которые пересекают площадку S (рис.1). Поток магнитной индукции может быть положительным и отрицательным. Знак потока зависит от выбора положительного направлении нормали к площадке S. Обычно, положительное направление нормали связывают с направлением обхода контура током. За положительное направление нормали принимают поступательное перемещение правого винта, при вращении его по току.
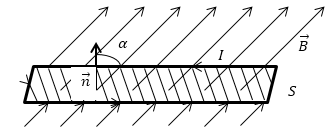
Рис. 1
В том случае, если магнитное поле неоднородно, S не является плоской, то поверхность можно разбить на элементарные площадки dS, которые рассматриваются как плоские, а поле на этой площадке можно считать однородным. В таком случае магнитный поток (dФ) можно через такую поверхность определить как:
\[dФ=BdScos\alpha =\overrightarrow{B}d\overrightarrow{S}\left(2\right).\]Тогда полный поток через поверхность S находится как:
\[Ф=\int\limits_S{BdScos\alpha =\int\limits_S{\overrightarrow{B}d\overrightarrow{S}}\left(3\right).}\]Основная единица измерения магнитного потока в системе СИ -- вебер (Вб). $1\ Вб=\frac{1Тл}{1м^2}$.
Связь магнитного потока и работы сил магнитного поля
Элементарную работу ($\delta A$), которую совершают силы магнитного поля можно выразить через элементарное изменение потока вектора магнитной индукции (dФ):
\[\delta A=IdФ\ \left(4\right).\]В том случае, когда проводник с током совершил конечное перемещение, а сила тока постоянна, то работа сил поля равна:
\[A=I\left(Ф_2-Ф_1\right)\left(5\right),\]где $Ф_1$ -- поток через контур в начале перемещения, $Ф_2$ -- поток через контур в конце перемещения.
Теорема Гаусса для магнитного поля
Суммарный магнитный поток через замкнутую поверхность S равен нулю:
\[\oint{\overrightarrow{B}d\overrightarrow{S}}=0\ (6)\ .\]Уравнение (6) справедливо для любых магнитных полей. Это уравнение аналог теоремы Остроградского - Гаусса в электростатике (в вакууме):
\[\oint{\overrightarrow{E}d\overrightarrow{S}}=\frac{q}{{\varepsilon }_0}\left(7\right).\]Уравнение (6) означает, что источником магнитного поля являются не магнитные заряды (их в природе не существует), а электрические токи. Данную теорему мы подробно рассматривали в разделе «Отсутствие в природе магнитных зарядов».
Задание: Недалеко от бесконечно длинного прямого проводника с током I находится квадратная рамка, по которой течет ток с силой $I'$. Сторона рамки равна $а$. Рамка лежит в плоскости с проводом (рис.2). Расстояние от ближайшей стороны рамки до проводника равно b. Найдите работу магнитной силы при удалении рамки из поля. Считать токи постоянными.
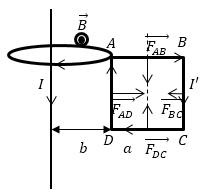
Рис. 2
Индукция магнитного поля длинного проводника с током в части, где расположена квадратная рамка, направлена на нас.
Решение:
При решении этой задачи необходимо помнить, что рамка с током находится в неоднородном поле, магнитная индукция убывает при удалении от провода.
В качестве основы для решения задачи используем формулу связи потока и работы:
\[A=I'\left(Ф_2-Ф_1\right)\left(1.1\right),\]$I'$- сила тока в рамке, $Ф_1$- поток через квадратную рамку, когда расстояние от ее стороны, ближайшей к проводу равна $b$. $Ф_2=0$, так как в конечном положении рамка вне магнитного поля по условию. Следовательно, формула (1.1) запишется как:
\[A=-I'Ф_1\left(1.2\right).\]Выберем направление нормали ($\overrightarrow{n}$) к квадратному контуру от нас (по правилу правого винта). Тогда для всех элементов поверхности, которая ограничена контуром квадратной рамки угол между нормалью $\overrightarrow{n}$ и вектором $\overrightarrow{B}$ равен $\pi $. Тогда формула для потока через поверхность рамки на расстоянии x от провода имеет вид:
\[dФ=-BdS=-B\cdot a\cdot dх=-\frac{{\mu }_0}{2\pi }Il\frac{dх}{х}\ \left(1.3\right),\]где индукция магнитного поля бесконечно длинного проводника с током силы I равна:
\[B=\frac{\mu_0}{2\pi х}Il\left(1.4\right).\]Следовательно, весь поток из (1.3) найдем как:
\[Ф_1=\int\limits_S{-\frac{{\mu }_0}{2\pi }Il\frac{dх}{х}}=-\frac{{\mu }_0}{2\pi }Il\int\limits^{b+a}_b{\frac{dх}{х}}=-\frac{{\mu }_0}{2\pi }Il\cdot ln\frac{b+a}{b}\left(1.5\right).\]Подставим формулу (1.5) в выражение (1.2) найдем искомую работу:
\[A=I'\frac{{\mu }_0}{2\pi }Il\cdot ln\frac{b+a}{b}.\]Ответ: $A=\frac{{\mu }_0}{2\pi }II'l\cdot ln\frac{b+a}{b}.$
Задание: Найдите силу, которая действует на рамку в предыдущем примере.
Решение:
Для того чтобы найти силу, которая действует на квадратную рамку с током в поле длинного провода положим, что под действием магнитной силы рамка сместилась на малое расстояние dx. В таком случае сила совершает работу равную:
\[\delta A=Fdx\ (2.1)\]Элементарную работу $\delta A$ с другой стороны выразим как:
\[\delta A=I'dФ\ \left(2.2\right).\]Выразим силу, используя (2.1) и (2.2), получим:
\[Fdx=I'dФ\ \to F=I'\frac{dФ}{dx}\left(2.3\right).\]Используя формулу, полученную в примере 1:
\[dФ=-\frac{{\mu }_0}{2\pi }Il\frac{dх}{х}\ \to \frac{dФ}{dx}=-\frac{{\mu }_0}{2\pi }\frac{Il}{х}\ \left(2.4\right).\]Подставим $\frac{dФ}{dx}$ в выражении для модуля силы (2.3), получим:
\[F=I'\frac{{\mu }_0}{2\pi }\frac{Il}{х}\left(2.5\right).\]На каждый элемент контура квадратной рамки действует сила (сила Ампера), всего на рамку действует четыре составляющих силы, однако, очевидно, что силы, которые действуют на стороны AB и DC равны по модулю и противоположны по направлению:
\[\overrightarrow{F_{AB}}+\overrightarrow{F_{DC}}=0\ (2.6)\]их сумма равна нулю, в таком случае, результирующая сила, приложенная к контуру будет:
\[\overrightarrow{F}=\overrightarrow{F_{AD}}+\overrightarrow{F_{BC}}\left(2.6\right).\]Эти силы, в соответствии с правилом левой руки, направлены вдоль одной прямой в противоположные стороны, то есть:
\[F=F_{AD}-F_{BC}\ \left(2.7\right).\]Найдем силу $F_{AD,}$ используя формулу (2.5), где $x=b$, получим:
\[F_{AD}=I'\frac{м_0}{2\pi}\frac{Il}{b}\left(2.8\right).\]Тогда $F_{BC}$ равна:
\[F_{BC}=I'\frac{{\mu }_0}{2\pi }\frac{Il}{b+a}\left(2.9\right).\]Искомая сила получается равной:
\[F=I'\frac{{\mu }_0}{2\pi }\frac{Il}{b}-I'\frac{{\mu }_0}{2\pi }\frac{Il}{b+a}={II}'\frac{{\mu }_0l}{2\pi }\left(\frac{1}{b}-\frac{1}{b+a}\right).\]Ответ: $F={II}'\frac{{\mu }_0l}{2\pi }\left(\frac{1}{b}-\frac{1}{b+a}\right).\ $Магнитные силы выталкивают рамку стоком, пока она сохраняет первоначальную ориентацию относительно поля провода.











