Потенциальная функция линейного тока. Связь с пондемоторными силами
Обозначим через Ф поток вектора магнитной индукции (магнитный поток) через произвольную поверхность S, которая опирается на контур L:
$\overrightarrow{n\ }$ - положительная нормаль к S, которая образует с направлением тока правовинтовую систему. Этот поток зависит только от расположения контура L, но не зависит от формы поверхности S. Используя определение векторного потенциала:
поток можно записать как:
Так мы получили, что магнитный поток Ф через контур L равен циркуляции векторного потенциала по заданному контуру. Если перемещать контур элементарная механическая работа $\delta А\ \ $сил $магнитного$ поля может быть представлена как:
где $\delta Ф$ -- увеличение магнитного потока через поверхность, связанную с контуром с током.
Формула (4) показывает, что работа пондемоторных сил магнитного поля при любом перемещении тока равна произведению изменения магнитного потока на силу тока. Следовательно, перемещения, при которых магнитный поток через контур не изменяется, не связаны с работой магнитного поля.
Введем обозначение:
В таком случае уравнение (4) примет вид:
где индекс I обозначает, что при определении приращения функции U силу тока считаем постоянной. В данном случае функция U выступает в роли потенциальной или силовой функции тока в магнитном поле. Следовательно, формула (6) значит, что работа пондемоторных сил магнитного поля равна убыли потенциальной функции тока.
Если функция U выражена в зависимости от «обобщенных» координат $q_i$, которые характеризуют положение контура с током, «обобщенная» пондемоторная сила ${\theta }_i$, которая действует на контур с током в направлении любой из координат $q_i,$ может быть представлена как:
Свойство (7) силовой функции U однако, не дает права отождествлять ее с потенциальной энергией магнитного поля. Так как при перемещении проводника с током в магнитном поле не только пондемоторные силы совершают работу, также выполняют работу электродвижущие силы. Значит, изменение энергии магнитного поля при перемещении проводника нельзя приравнять к работе пондемоторных сил поля.
Введение потенциальной функции тока облегчает рассмотрение пондемоторных сил, которые действуют на токи в магнитном поле, так как это позволяет исключить сложное суммирование сил, которые действуют на отдельные элементы тока.
Так, например, из уравнения (6) и (7) следует, что устойчивое равновесие контура с постоянным током соответствует минимуму потенциальной функции U или по (5) максимуму магнитного потока Ф.
Потенциальная функция тока для объемных токов
В том случае, когда нельзя не учитывать изменением магнитной индукции по сечению тока от линейных токов переходят к объемным токам. Для этого в уравнение (5) подставим вместо магнитного потока правую часть уравнения (3), получим:
Затем перейдем к объемным токам, тогда потенциальную функцию тока определяют как:
Задание: Рамка находится в однородном магнитном поле с индукцией B и закреплена так, что может вращаться вокруг своей оси (рис.1). Ее площадь равна S. По ней течет ток силы I. Угол $\alpha $ -- между положительной нормалью к рамке и вектором $\overrightarrow{B}.$ В каком положении рамка находится в состоянии устойчивого равновесия?
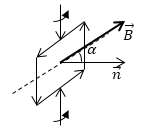
Рис. 1
Решение:
Магнитный поток (Ф) через рамку равен:
\[Ф=BScos\alpha \ \left(1.1\right).\]тогда потенциальная функция тока будет иметь вид:
\[U=-ISBcos\alpha \left(1.2\right).\]Момент сил, приложенных к рамке сил, который стремится повернуть рамку, равен:
\[M=-\frac{\partial U}{\partial \alpha }=ISBsin\alpha \left(1.3\right).\]Положения равновесия рамки соответствует M=0. То есть $\alpha =0,\ \alpha =\pi .$ Первый угол соответствует минимуму потенциальной функции, второй угол максимуму потенциальной функции. Следовательно, только первый угол соответствует устойчивому равновесию.
Ответ: Пондемоторные силы магнитного поля стремятся повернуть рамку с током так, чтобы положительная нормаль совпадала с линиями поля.
Задание: Рассмотрим взаимодействие двух замкнутых линейных токов $I_1\ и\ I_2$, которые обтекают контуры $L_1\ и\ L_2$ соответственно. Магнитный поток, который второй ток образует через контур первого тока, равен $Ф_{21}=I_2L_{21}$, $Ф_{12}=I_1L_{12}$- магнитный поток, первого тока через контур второго тока, здесь $L_{21}=L_{12}$ -- называют коэффициентами взаимной индукции контуров $L_1\ и\ L_2$. Коэффициенты взаимной индукции зависят от конфигурации, взаимного расположения контуров и направления их обхода. Силы токов в контурах постоянны. Запишите выражения для пондемоторных сил, которые действуют на токи и выражение для соответствующей им работы.
Решение:
Запишем выражения для потенциальных функций токов. Для тока $I_1$ в поле тока $I_2\ $получим:
\[U_{21}=-I_2Ф_{21}=-L_{21}{I_2I}_1\ \left(2.1\right).\]Для тока $I_2$ в поле тока $I_1\ $имеем:
\[U_{12}=-I_1Ф_{12}=-L_{12}{I_1I}_2\ \left(2.2\right).\]Так как$\ L_{12}$=$L_{12}$, следовательно, $U_{21}=U_{12}$. Обобщенные пондемоторные силы ${\theta }_i$ равны:
\[{\theta }_i=-\frac{{\left(\partial U\right)}_I}{\partial q_i}={I_1I}_2\frac{\partial L_{12}}{\partial q_i}\left(2.3\right).\]Так как токи постоянны, то получаем:
\[\theta ={I_1I}_2\frac{\partial L_{12}}{\partial q_i}\left(2.4\right).\]Работа механических сил равна:
\[\delta A=-{\left(\delta U_{12}\right)}_I={I_1I}_2\delta L_{12}\left(2.5\right).\]Механическое взаимодействие замкнутых токов удовлетворяет принципу «действие равно противодействию», так как силы, которые испытывают каждый ток, определены одинаковыми функциями $U_{12}=U_{21}$, которые зависят только от относительного расположения контуров.
Ответ: $\theta ={I_1I}_2\frac{\partial L_{12}}{\partial q_i}.\ \ \delta A={I_1I}_2\delta L_{12}.$












