Определение элементарного замкнутого тока
Элементарным замкнутым током называют линейный ток, который обтекает поверхность с бесконечно малыми в физическом смысле линейными размерами.
Итак, элементарным током мы будем называть замкнутый ток, который удовлетворяет следующим условиям:
- Размеры контура бесконечно малы в сравнении с расстоянием до точек, в которых необходимо рассмотреть поле.
- Величины, которые характеризуют внешнее поле, постоянны (Точнее постоянны значения магнитной индукции и ее пространственные производные). Для любого замкнутого тока можно создать условия, при которых его считают элементарным.
Векторный потенциал элементарного тока
Выберем контур в виде параллелограмма, стороны которого $l_1,l_2,\ l_3,l_4\ $(рис.1). Начало координат поместим в точку О на поверхности внутри параллелограмма. Так как параллелограмм бесконечно малый, то конкретное место положения точки значения не имеет.
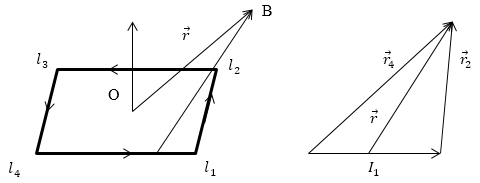
Рис. 1
Векторный потенциал магнитного поля ($\overrightarrow{A}$) в точке B с радиус-вектором $\overrightarrow{r}$ равен:
\[\overrightarrow{A}\left(\overrightarrow{r}\right)=\frac{{\mu }_0}{4\pi }I\int\limits_{l_1l_2l_3l_4}{\frac{\overrightarrow{dl}}{r}}\left(1\right).\]Так как параллелограмм маленький, то значение r можно считать постоянным и равным расстоянию от середины стороны параллелограмма до точки, в которой ищем поле. Соответственно перепишем уравнение (1):
\[\overrightarrow{A}\left(\overrightarrow{r}\right)=\frac{{\mu }_0}{4\pi }I\left(\frac{1}{r_1}\int\limits_{l_1}{\overrightarrow{dl}}+\frac{1}{r_2}\int\limits_{l_2}{\overrightarrow{dl}}+\frac{1}{r_3}\int\limits_{l_3}{\overrightarrow{dl}}+\frac{1}{r_4}\int\limits_{l_4}{\overrightarrow{dl}}\right)=\frac{{\mu }_0}{4\pi }I\left(\frac{I_1}{r_1}+\frac{I_2}{r_2}+\frac{I_3}{r_3}+\frac{I_4}{r_4}\right)(2).\]Учтем, что:
\[I_1=-I_3,\ I_2=-I_4\left(3\right).\]Для того чтобы преобразовать выражение (2) найдем:
\[\frac{I_1}{r_1}+\frac{I_3}{r_3}=I_1\left(\frac{r_3-r_1}{r_1r_3}\right)\approx \frac{I_1\left(-{\overrightarrow{l}}_2\cdot \overrightarrow{r}\right)}{r^3},\] \[\frac{I_2}{r_2}+\frac{I_4}{r_4}=I_2\left(\frac{r_4-r_2}{r_2r_4}\right)\approx \frac{I_2\left({\overrightarrow{l}}_1\cdot \overrightarrow{r}\right)}{r^3}\left(4\right),\]где бесконечно малыми величинами высоких порядков пренебрегаем. На рис.1 показаны геометрические построения для разъяснения того как получены равенства:
\[\overrightarrow{r_4}=\overrightarrow{l_1}+\overrightarrow{r_2}\left(5\right).\]Из равенства (5) получим:
\[{r_4}^2={l_1}^2+{r_2}^2+2\overrightarrow{l_1}\overrightarrow{r_2}\left(6\right).\]Из уравнения (6) получим:
\[{r_4}^2-{r_2}^2={l_1}^2+2\overrightarrow{l_1}\overrightarrow{r_2}\to r_4-r_2=\frac{{l_1}^2+2\overrightarrow{l_1}\overrightarrow{r_2}}{r_4+r_2}\approx \frac{\overrightarrow{l_1}\overrightarrow{r_2}}{r}\left(7\right).\]В выражении (7) мы сохранили члены только первого порядка малости по $\overrightarrow{l_1}$. Таким образом, получено выражение (4). С учетом (4) выражение для векторного магнитного потенциала (2) примет вид:
\[\overrightarrow{A}\left(\overrightarrow{r}\right)=\frac{{\mu }_0}{4\pi }\frac{I}{r^3}\left[I_2\left({\overrightarrow{l}}_1\overrightarrow{r}\right)-I_1\left({\overrightarrow{l}}_2\overrightarrow{r}\right)\right]=\frac{{\mu }_0}{4\pi }\frac{I}{r^3}\left({\overrightarrow{l}}_1\times {\overrightarrow{l}}_2\right)\times \overrightarrow{r}\left(8\right),\]где использовано известное равенство их векторной алгебры:
\[\overrightarrow{A}\times \left(\overrightarrow{B}\times \overrightarrow{C}\right)=\overrightarrow{B}\left(\overrightarrow{A}\overrightarrow{C}\right)-\overrightarrow{C}\left(\overrightarrow{A}\overrightarrow{B}\right)\left(9\right).\]Используем то, что вектор элемента поверхности, которая обтекается током, равна:
\[{\overrightarrow{l}}_1\times {\overrightarrow{l}}_2=\overrightarrow{S}\left(10\right).\]Перепишем уравнение (8), получим:
\[\overrightarrow{A}\left(\overrightarrow{r}\right)=\frac{\mu_0}{4\pi}\frac{I\overrightarrow{S} \times \overrightarrow{r}}{r^3}\left(11\right).\]Магнитный момент элементарного тока
Произведение:
\[I\overrightarrow{S}=\overrightarrow{p_m}(12)\]называется магнитным моментом элементарного тока.
Из (12) очевидно, что эта величина по модулю равна произведению силы тока, который течет в контуре на площадь, которая охвачена им. Направление магнитного момента совпадает с положительной нормалью к поверхности S. Если использовать в записи векторного магнитного потенциала магнитный момент элементарного тока, то выражение (11) примет вид:
\[\overrightarrow{A}\left(\overrightarrow{r}\right)=\frac{{\mu }_0}{4\pi }\frac{\overrightarrow{p_m}\times \overrightarrow{r}}{r^3}\left(13\right).\]Основная единица измерения магнитного момента - $А\cdot м^2.$
Задание: Определите силу тока (I) в витке, если магнитный момент витка $0.1\ А\cdot м^2$. Диаметр витка равен d=0,01 м.
Решение:
За основу решения задачи примем определение модуля магнитного момента витка с током:
\[IS=p_m\left(1.1\right).\]Площадь витка S равна:
\[S=\pi R^2=\pi \frac{d^2}{4}\left(1.2\right).\]Из (1.1) выразим силу тока, подставим S из выражения (1.2) получим:
\[I=\frac{p_m}{S}=\frac{{4p}_m}{d^2\pi }\]Данные в условии задачи представлены в системе СИ, следовательно, можно провести вычисления:
\[I=\frac{4\cdot 0,1}{{0,01}^2\cdot 3,14}=1270(А).\]Ответ: $I=1270\ А.$
Задание: Найдите магнитный момент $p_m\ $кругового витка с током если модуль вектора магнитной индукции в точке А равен В. Расстояние от центра кольца до точки А равно d (рис.2). Считайте ток элементарным.
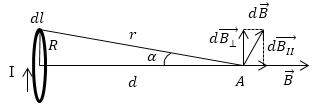
Рис. 2
Решение:
Выделим на круговом витке в током элемент тока $Idl$ . Для этого элемента запишем закон Био-Савара -- Лапласа для вакуума, чтобы найти поле, которое создает этот ток в точке А:
\[dB=\frac{{\mu }_0}{4\pi }\frac{Idl}{r^2}=\frac{{\mu }_0}{4\pi }\cdot \frac{Idl}{R^2+d^2}\ \left(2.1\right),\]где $r$ -- расстояние от $dl$ до точки A, $r^2=R^2+d^2,\ R$ -- радиус витка с током.
\[{dB}_{II}=Bsin\alpha ,\ sin\alpha =\frac{R}{\sqrt{R^2+d^2}}\left(2.2\right).\]Подставим (2.1) в (2.2) получим:
\[{dB}_{II}=\frac{\mu_0}{4\pi}\frac{IRdl}{{\left(R^2+d^2\right)}^{{3}/{2}}}\left(2.3\right).\]Используя принцип суперпозиции найдем полное поле, которое создает элементарный ток (виток с током) в точке А:
\[B_{II}=\int\limits^{2\pi R}_0{\frac{{\mu }_0}{4\pi }\frac{IRdl}{{\left(R^2+d^2\right)}^{{3}/{2}}}}=\frac{{\mu }_0}{2}\cdot \frac{IR^2}{{\left(R^2+d^2\right)}^{{3}/{2}}}\left(2.4\right).\]В силу симметрии суммарный вклад в магнитную индукцию составляющей $B_{\bot }равен\ нулю$. Следовательно, можно запить, что магнитная индукция поля в точке А равна:
\[B=\frac{{\mu }_0}{2}\cdot \frac{IR}{{\left(R^2+d^2\right)}^{{3}/{2}}}\left(2.5\right).\]По условию, мы имеем дело с элементарным током, следовательно, $R\ll d$. В таком случае, (2.5) преобразуется в формулу:
\[B=\frac{{\mu }_0}{2}\cdot \frac{IR^2}{d^3}\left(2.6\right).\]Магнитный момент контура определен как:
\[p_m=IS=I\pi R^2\left(2.7\right).\]Из (2.6) получим, что:
\[IR^2=\frac{2Bd^3}{{\mu }_0}\to p_m=\frac{2\pi Bd^3}{{\mu }_0}.\]Ответ: $p_m=\frac{2\pi Bd^3}{{\mu }_0}.$











