История развития электромагнетизма
Примерно до середины XIX века все электрические, магнитные явления ученые рассматривали в отдельности, считая их, независимыми друг от друга. Ситуация в физике начала принципиально с открытием гальванизма, который показал связь между химическими и физическими явлениями.
Открытие электромагнетизма связывают с именем Х.К. Эрстеда. Он увлекался немецкой классической философией, в основе которой лежит учение о всеобщей связи и диалектике природы, и много думал о связи теплоты, света, электричества и магнетизма. Результатом своих размышлений Эрстед сделал труд под названием: «Исследование о тождестве электрических и химических сил». Позднее Эрстед открыл, что вокруг проводника с током возникает магнитное поле, которое в свою очередь действует на ток. Если говорить в современных терминах: он установил, что магнитные силовые линии окружают проводник, по которому идет ток. Ток - вихрь магнитного поля. Так можно сформулировать первый основной закон электродинамики -- смысл открытия Эрстеда. Данное открытие привлекло ученых Европы, вызвало сильный резонанс.
Следом за Эрстедом экспериментально установили свой закон, описывающий порождение магнитного поля током Био и Савар. Лаплас математически записал данный закон. Так для замкнутого тока I закон Био-Савара --Лапласа имеет вид:
где $\overrightarrow{r}$ -- радиус-вектор, проведенный от элемента тока $Id\overrightarrow{l}$ к точке, в которой ищется индукция магнитного поля ($\overrightarrow{B}$). Интегрирование проводят по замкнутому контуру тока. Считается, что ток является линейным. Для объемных токов закон Био -- Савара-Лапласа записывается как:
В формуле (2) интегрирование проводят по всем областям пространства, где присутствуют объемные токи, $\overrightarrow{j}$- плотность тока.
Следующим ученым, которого здесь следует отметить, является Ампер, который внес очень существенный вклад в развитие идей электромагнетизма. Он первым установил, что проводники по которым течет электрический ток, взаимодействуют механически (притягиваются или отталкиваются). Ампер подчеркивал, что это взаимодействие токов коренным образом отличается от того, что проявляется в электростатике. Уже тогда Ампер выдвинул идею устройства телеграфа с помощью электромагнетизма. Эта идея была реализована гораздо позднее американским изобретателем Морзе. Ампер пришел к заключению о том, что магнитный листок эквивалентен круговому току и представил магнит как совокупность электрических токов, которые лежат в плоскостях, перпендикулярных к линии, которая соединяет полюса магнита. Он показал, что соленоид эквивалентен магниту. Ампер выдвинул мысль об отсутствии «магнитных жидкостей» (магнитных агентов). Ампер первым пришел к идее свести все явления магнетизма к электродинамическим взаимодействиям. Формула (закон) Ампера стоит в ряду важных законов элементарной электродинамики:
Формула (3) показывает, что сила $d\overrightarrow{F}$ в магнитном поле с индукцией $\overrightarrow{B}$ действует на элемент с током $Id\overrightarrow{l}$. Важно то, что взаимодействие элементарных токов не удовлетворяют третьему закону Ньютона. Это новый тип взаимодействий, что и заметил Ампер. Но Ампер еще не знал о существовании поля.
Вопросами полей вплотную занимался М. Фарадей. Он увидел вихревой характер магнитного поля. Связь, установленную Фарадеем между электричеством и магнетизмом, позднее математически описал Максвелл с помощью равенства:
где $\mathcal E$ ЭДС индукции, $Ф$ -- магнитный поток, который охватывает проводник с током, в котором индуцируется ток. Формула (4) означает, что магнитное поле окружено вихревым магнитным полем. В векторной форме данный закон имеет вид:
Исследование электрических и магнитных свойств вещества привели Фарадея к идее существования магнитного поля. Что явилось фундаментальным открытием. Фарадей разработал методику исследования нового вида материи.
Если поля статические (независимые от времени), то можно рассматривать электрическое и магнитное поля отдельно друг от друга. Ситуация изменяется радикально, если поля меняются во времени. Переменные электрические и магнитные поля взаимозависимы, поэтому вводится понятие электромагнитного поля и этому полю посвящен раздел, который называют «электромагнетизмом».
Магнитостатика
Магнитостатика -- это раздел электродинамики, который изучает свойства магнитного поля, которое порождается постоянным током.
Основными законами, которые используются в данном разделе физики, являются: закон Ампера (3) во всех его модификациях (для элементарных токов, для параллельных прямолинейных токов) и закон Био-Савара-Лапласа (2).
На основании закона Ампера устанавливают единицы силы тока в системах СИ и СГСМ. Так как ампер равен силе постоянного тока, который при течении по двум параллельным бесконечно длинным прямолинейным проводникам бесконечно малого кругового сечения, находящихся на расстоянии 1м друг от друга в вакууме вызывает силу взаимодействия этих проводников равную $2\cdot {10}^{-7}Н$ на каждый метр длины.
Закон Био-Савара-Лапласа очень часто используют для расчета магнитных полей, то есть находят силовую характеристику магнитного поля ($\overrightarrow{B}$).
Задание: Найдите индукцию магнитного поля, которое создается прямолинейным участком проводника длиной $l$, по которому течет ток силы $I\ (рис.1)$. Считать, что известны величины b, ${\alpha }_1\ и\ б_2$.
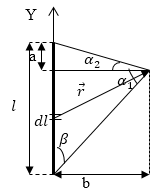
Рис. 1
Решение:
Индукция магнитного поля от каждого элемента проводника с током ($Id\overrightarrow{l}$) направлена перпендикулярно плоскости рисунка и по закону Био-Савара-Лапласа равна:
\[\overrightarrow{dB}=\frac{{\mu }_0}{4\pi }\frac{I\left[d\overrightarrow{l}\overrightarrow{r}\right]}{r^3}\left(1.1\right),\]где $\overrightarrow{r}$ -- радиус-вектор, проведенный от элемента тока $Id\overrightarrow{l}$ к точке, в которой ищется индукция магнитного поля ($\overrightarrow{B}$). Так как в числителе выражения (1.1) мы имеем векторное произведение, исходя их рис.1 запишем:
\[\left|d\overrightarrow{l}\times \overrightarrow{r}\right|=dl\cdot rsin\left(\widehat{d\overrightarrow{l},\overrightarrow{r}}\right)dl\cdot rsin\beta =\left(dy\right)b\ \left(1.2\right),\]где $dy$ -- приращение координаты. Подставим полученное в (1.2) в закон (1.1), применим принцип суперпозиции для магнитных полей, получим:
\[B=\frac{{\mu }_0Ib}{4\pi }\int\limits^a_{-(l-a)}{\frac{dy}{{\left(b^2+y^2\right)}^{\frac{3}{2}}}}=\frac{{\mu }_0I}{4\pi b}\left(sin{\alpha }_1+sin{\alpha }_2\right).\]Ответ: $B=\frac{{\mu }_0I}{4\pi b}\left(sin{\alpha }_1+sin{\alpha }_2\right).$
Задание: По прямому, круглому соленоиду течет ток (I). Соленоид имеет длину L и состоит из n витков тонкого провода. Витки плотно прилегают друг к другу. Найдите индукцию на оси соленоида, если считать соленоид бесконечно длинным.
Решение:
По условию задачи витки с током плотно прилегают друг к другу, можно считать, что каждый виток создает поле на оси соленоида, которое можно записать как:
\[B=\frac{{\mu }_0I}{2}\frac{R^2}{{\left(R^2+x^2\right)}^{\frac{3}{2}}}\left(2.1\right),\]где $R$ -- радиус витка, $x$ -- расстояние от центра витка, до точки, в которой рассматривается поле.
Плотность намотки равна $\frac{n}{L}.\ $Можно считать, что на длине dx соленоида течет ток равный $\left(\frac{In}{L}\right)dx.$ Поместим начало системы координат в точку, совпадающую с половиной длины соленоида. Используем формулу для витка (2.1), получим, что индукция магнитного поля на оси соленоида в точке x равна:
\[B_x=\frac{{\mu }_0InR^2}{2L}\int\limits^{\frac{L}{2}}_{-\frac{L}{2}}{\frac{dx'}{{\left(R^2+{\left(x-x'\right)}^2\right)}^{\frac{3}{2}}}}=\frac{{\mu }_0InR^2}{2L}\left[\frac{-x+\frac{L}{2}}{{\left[{\left(x-\frac{L}{2}\right)}^2+R^2\right]}^{\frac{1}{2}}}+\frac{x+\frac{L}{2}}{{\left[{\left(x+\frac{L}{2}\right)}^2+R^2\right]}^{\frac{1}{2}}}\right](2.2).\]Если мы имеем дело с очень длинным соленоидом, то при $(L\to \infty )$ в точках $x\ll \frac{L}{2}$ в пределе от выражения в (2.2) получаем:
\[{\mathop{lim}_{L\to \infty } B_x\ }=\frac{{\mu }_0In}{L}.\]Ответ: $B_x=\frac{м_0InR^2}{2L}\left[\frac{-x+\frac{L}{2}}{{\left[{\left(x-\frac{L}{2}\right)}^2+R^2\right]}^{\frac{1}{2}}}+\frac{x+\frac{L}{2}}{{\left[{\left(x+\frac{L}{2}\right)}^2+R^2\right]}^{\frac{1}{2}}}\right].\ $При $L\to \infty \ B_x=\frac{{\mu }_0In}{L}.$











