Определение магнитного поля. Его источники
Магнитное поле - одна из форм электромагнитного поля, которое действует только на движущиеся тела, которые имеют электрический заряд или намагниченные тела не зависимо от их движения.
Источниками этого поля являются постоянные электрические токи, движущиеся электрические заряды (телами и частицами), намагниченные тела, переменные электрические поля. Источниками постоянного магнитного поля являются постоянные токи.
Свойства магнитного поля
Во времена, когда изучение магнитных явлений только началось, исследователи особенное внимание уделяли тому, что существуют полюса в намагниченных брусках. В них магнитные свойства проявлялись особенно ярко. При этом четко было видно, что полюса магнита различны. Разноименные полюса притягивались, а одноименные отталкивались. Гильберт высказал идею о существовании «магнитных зарядов». Эти представление подержал и развил Кулон. На основе опытов Кулона силовой характеристикой магнитного поля стала сила, с которой магнитное поле действует на магнитный заряд, равный единице. Кулон же обратил внимание на существенные различия между явлениями в электричестве и магнетизме. Различие проявляется уже в том, что электрические заряды можно разделить и получить тела с избытком положительного или отрицательного заряда, тогда как невозможно разделить северный и южный полюса магнита и получить тело только с одним полюсом. Из невозможности деления магнита на исключительно «северный» или «южный» Кулон решил, что два эти вида зарядов неразрывны в каждой элементарной частице намагничивающего вещества. Так, было признано, что каждая частица вещества - атом, молекула или их группа -- есть нечто вроде микро магнита с двумя полюсами. Намагничивание тела при этом -- процесс ориентации его элементарных магнитов под влиянием внешнего магнитного поля (аналог поляризации диэлектриков).
Взаимодействие токов реализуется посредством магнитных полей. Эрстед обнаружил, что магнитное поле возбуждается током и оказывает ориентирующее действие на магнитную стрелку. У Эрстеда проводник с током был расположен над магнитной стрелкой, которая могла вращаться. Когда ток шел в проводнике, стрелка поворачивалась перпендикулярно проволоке. Смена направления тока вызывало переориентацию стрелки. Из опыта Эрстеда следовало, что магнитное поле имеет направление и должно характеризоваться векторной величиной. Эту величину назвали магнитной индукцией и обозначили: $\overrightarrow{B}.$ $\overrightarrow{B}$ аналогичен вектору напряженности для электрического поля ($\overrightarrow{E}$). Аналогом вектора смещения $\overrightarrow{D}\ $для магнитного поля стал вектор $\overrightarrow{H}$- называемый вектором напряжённости магнитного поля.
Магнитное поле воздействует только на движущийся электрический заряд. Магнитное поле рождается движущимися электрическими зарядами.
Магнитное поле движущегося заряда. Магнитное поле витка с током. Принцип суперпозиции
Магнитное поле электрического заряда, который движется с постоянной скоростью, имеет вид:
\[\overrightarrow{B}=\frac{{\mu }_0}{4\pi }\frac{q\left[\overrightarrow{v}\overrightarrow{r}\right]}{r^3}\left(1\right),\]где ${\mu }_0=4\pi \cdot {10}^{-7}\frac{Гн}{м}(в\ СИ)$ -- магнитная постоянная, $\overrightarrow{v}$ -- скорость движения заряда, $\overrightarrow{r}$ -- радиус вектор, определяющий местоположение заряда, q -- величина заряда, $\left[\overrightarrow{v}\overrightarrow{r}\right]$- векторное произведение.
Магнитная индукция элемента с током в системе СИ:
\[dB=\frac{{\mu }_0}{4\pi }\frac{Idlsin \vartheta}{r^2}\left(2\right),\]где$\ \overrightarrow{r}$- радиус-вектор, проведенный из элемента тока в рассматриваемую точку, $\overrightarrow{dl}$- элемент проводника с током (направление задано направление тока), $\vartheta$ -- угол между $\overrightarrow{dl}$ и $\overrightarrow{r}$. Направление вектора $\overrightarrow{dB}$ -- перпендикулярно к плоскости, в которой лежат $\overrightarrow{dl}$ и $\overrightarrow{r}$. Определяется правилом правого винта.
Для магнитного поля выполняется принцип суперпозиции:
\[\overrightarrow{B}=\sum{{\overrightarrow{B}}_i\left(3\right),}\]где ${\overrightarrow{B}}_i$ -- отдельные поля, которые порождаются движущимися зарядами, $\overrightarrow{B}$ -- суммарная индукция магнитного поля.
Задание: Найдите отношение сил магнитного и кулоновского взаимодействия двух электронов, которые движутся с одинаковыми скоростями $v$ параллельно. Расстояние между частицами постоянно.
Решение:
Будем считать, что один электрон поле создает (и магнитное и электрическое), а другой в нем движется. Тогда на электрон, который движется в поле, действует со стороны магнитного поля сила равная (система СИ):
\[\overrightarrow{F_m}=q\left[\overrightarrow{v}\overrightarrow{B}\right]\left(1.1\right).\]Поле, которое создает второй движущийся электрон равно:
\[\overrightarrow{B}=\frac{{\mu }_0}{4\pi }\frac{q\left[\overrightarrow{v}\overrightarrow{r}\right]}{r^3}\left(1.2\right).\]Пусть расстояние между электронами равно $a=r\ (постоянно)$. Используем алгебраическое свойство векторного произведения (тождество Лагража ($\left[\overrightarrow{a}\left[\overrightarrow{b}\overrightarrow{c}\right]\right]=\overrightarrow{b}\left(\overrightarrow{a}\overrightarrow{c}\right)-\overrightarrow{c}\left(\overrightarrow{a}\overrightarrow{b}\right)$))
\[{\overrightarrow{F}}_m=\frac{{\mu }_0}{4\pi }\frac{q^2}{a^3}\left[\overrightarrow{v}\left[\overrightarrow{v}\overrightarrow{a}\right]\right]=\left(\overrightarrow{v}\left(\overrightarrow{v}\overrightarrow{a}\right)-\overrightarrow{a}\left(\overrightarrow{v}\overrightarrow{v}\right)\right)=-\frac{{\mu }_0}{4\pi }\frac{q^2\overrightarrow{a}v^2}{a^3}\ ,\]$\overrightarrow{v}\left(\overrightarrow{v}\overrightarrow{a}\right)=0$, так как $\overrightarrow{v\bot }\overrightarrow{a}$.
Модуль силы $F_m=\frac{{\mu }_0}{4\pi }\frac{q^2v^2}{a^2},\ $где $q=q_e=1,6\cdot 10^{-19}Кл$.
Модуль силы Кулона, которая действует на электрон, в поле равна:
\[F_q=\frac{q^2}{{4\pi {\varepsilon }_0a}^2}.\]Найдем отношение сил $\frac{F_m}{F_q}$:
\[\frac{F_m}{F_q}=\frac{{\mu }_0}{4\pi }\frac{q^2v^2}{a^2}:\frac{q^2}{{4\pi {\varepsilon }_0a}^2}={\mu }_0{{\varepsilon }_0v}^2.\]Ответ: $\frac{F_m}{F_q}={\mu }_0{{\varepsilon }_0v}^2.$
Задание: По витку с током в виде окружности радиуса R циркулирует постоянный ток силы I. Найдите магнитную индукцию в центре окружности.
Решение:
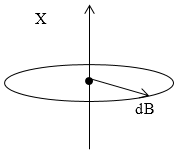
Рис. 1
Выберем на проводнике с током элементарный участок (рис.1), в качестве основы для решения задачи используем формулу индукции элемента витка с током:
\[dB=\frac{{\mu }_0}{4\pi }\frac{Idlsin \vartheta}{r^2}\left(2.1\right),\]где$\ \overrightarrow{r}$- радиус-вектор, проведенный из элемента тока в рассматриваемую точку, $\overrightarrow{dl}$- элемент проводника с током (направление задано направление тока), $\vartheta$ -- угол между $\overrightarrow{dl}$ и $\overrightarrow{r}$. Исходя из рис. 1 $\vartheta=90{}^\circ $, следовательно (2.1) упростится, кроме того расстояние от центра окружности (точки, где мы ищем магнитное поле) элемента проводника с током постоянно и равно радиусу витка (R), следовательно имеем:
\[dB=\frac{{\mu }_0}{4\pi }\frac{Idl}{R^2}\left(2.2\right).\]От всех элементов тока будет образовываться магнитные поля, которые направлены по оси x. Это значит, что результирующий вектор индукции магнитного поля можно найти как сумму проекций отдельных векторов$\ \ \overrightarrow{dB}.$ Тогда по принципу суперпозиции полную индукцию магнитного поля можно получить, если перейти к интегралу:
\[B=\oint{dB\ \left(2.3\right).}\]Подставим (2.2) в (2.3), получим:
\[B=\frac{{\mu }_0}{4\pi }\frac{I}{R^2}\oint{dl}=\frac{{\mu }_0}{4\pi }\frac{I}{R^2}2\pi R=\frac{{\mu }_0}{2}\frac{I}{R}.\]Ответ: $B$=$\frac{{\mu }_0}{2}\frac{I}{R}.$











