Амплитудная зонная пластинка
Колебания зон Френеля, которые являются четными и нечетными, существуют в противофазе, это значит, что они ослабляют друг друга. В том случае, если на пути распространения волны света расположить пластинку, которая будет перекрывать все четные (или все нечетные) зоны, то в таком случае интенсивность света в некоторой точке $A$ существенно возрастет. Подобная пластинка называется зонной. Она действует на подобии собирающей линзы. Рис. 1 изображает зонную пластинку, которая перекрывает четные зоны. Данная пластинка называется амплитудной зонной пластинкой.
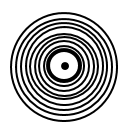
Рисунок 1.
В самом простом случае зонная пластинка представляет собой стеклянную пластинку, на которую нанесена система прозрачных и непрозрачных колец, строящихся по принципу расположения зон Френеля, что означает: радиусы колец определяются с помощью формул для зон Френеля:
где $a$ - расстояние от точечного источника света до зонной пластинки, $b$ - расстояние от точки наблюдения на линии, которая соединяет источник света и точку наблюдения.
Если зонную пластинку расположить на расстоянии $a$ от точечного источника и $b$ - от точки наблюдения на линии, которая соединяет эти две точки, то для света длиной волны $\lambda $ зонная пластинка перекроет четные зоны и свободными останутся нечетные и центральная.
Как результат, амплитуда суммарных колебаний равна:
и она больше, чем при условии, что волна распространяется свободно.
Интенсивность света больше при этом в четыре раза.
Фазовая зонная пластинка
Большего эффекта достигают, если изменяют фазу колебаний на $\pi $. Это осуществляется при использовании прозрачной пластинки с переменной толщиной, которая подобрана в местах, соответствующих четным и нечетным зонам. Такая зонная пластинка называется фазовой. В сравнении с амплитудной зонной пластинкой фазовая пластинка дает дополнительное увеличение амплитуды в два раза, интенсивности -- в четыре раза.
Допустим, что мы закрыли все нечетные зоны, оставили открытыми все четные. Амплитуда световой волны, которая проходит через пластинку на оси в токе А может рассчитываться с использованием спирали Френеля (рис.2).
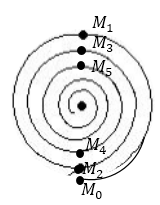
Рисунок 2.
Амплитуда от нулевой открытой круглой зоны задана вектором $\overrightarrow{M_0M_1}$, от второй открытой зоны (кольцевой) может быть определена вектором $\overrightarrow{M_2M_3}$, от четвертой - $\overrightarrow{M_1M_5}$ и так далее. Эти векторы имеют одинаковые направления, что означает, фазы их комплексных амплитуд отличны на 2$\pi n$ (где $n$ - целое число). Следовательно, можно сделать вывод о том, что реализуется интерференция волн с усилением. Получается, что в исследуемой токе $A$ происходит существенное усиление световой интенсивности (свет в точке фокусируется). Поведение зонной пластинки аналогично поведению линзы.
Допустим, что падающие на пластинку лучи параллельны ($R\to \infty ,\ где\ R-радиус\ кривизны\ фронта\ сферической\ волны\ $). В таком случае, точка на оси, в которой собираются лучи, ведет себя как фокус линзы, положение линзы совпадает с положением зонной пластинки, если фокусное расстояние линзы $(f)$ равно:
где $l$ - расстояние от точки пересечения фронта волны с прямой, которая соединяет источник сферической волны и рассматриваемую точку $A$ до самой точки $A$. $r_m-$радиус зоны Френеля номера $m$ (целое число) при $R\to \infty $ равна:
где $\lambda $ - длина волны света. Соответственно, фокусное расстояние, можно рассчитать как:
Радиус зоны номер m при $R\ne \infty $ равен:
Выражение (4) часто представляют в виде:
Формула (7) показывает, что зонная пластинка действует, как собирательная линза. Используя ее можно формировать изображение, что является подтверждением на опыте правильности идеи зон Френеля. В отличие от линзы зонная пластинка имеет несколько фокусов:
где $n$ - целые числа (положительные и отрицательные).
Задание: Каков радиус первой зоны Френеля, если на зонную пластинку падает плоская монохроматическая волна света длиной $\lambda =0,5\ мкм$. Расстояние от пластинки до места наблюдения принять равным $1м$.
Решение:
За основу решения задачи примем формулу, которая определяет радиус зоны Френеля номера $m$, для плоской волны:
\[r_m=\sqrt{mb\lambda }\left(1.1\right),\]где $b$- расстояние от пластинки до места наблюдения, $m=1$. Переведем в систему СИ длину волны света:
$\lambda =0,5\ мкм=0,5\cdot {10}^{-6}м$. Поведем вычисления:
\[r_1=\sqrt{1\cdot 1\cdot 0,5\cdot {10}^{-6}}\approx 0,707\cdot {10}^{-3}\left(м\right).\]Ответ: $r_1=707\ мкм$.
Задание: Где расположено изображение источника света, который находится в бесконечности, если изображение источника света, расположенного на расстоянии $a=2\ м$ от зонной пластинки, находится в $b=1$ метре от ее поверхности?
Решение:
Источник света, который находится на расстоянии $a=2\ м$ от зонной пластинки, будем считать источником сферических волн, следовательно, для вычисления радиусов зон Френеля применяем формулу:
\[{r_m}^2=\frac{ab}{a+b}m\lambda \left(2.1\right).\]Если источник света удален на бесконечность, то световую волну, которая падает на зонную пластинку можно считать плоской волной, тогда радиусы зон Френеля найдем как:
\[{r_m}^2=m\lambda b'\left(2.2\right),\]где $b'$- расстояние от пластинки до изображения источника.
В выражениях (2.1) и (2.2) левые части равны, следовательно, приравняем правые части, получим:
\[\frac{ab}{a+b}m\lambda =m\lambda b'\left(2.3\right).\]Из выражения (2.3) выразим искомую величину $b'$, получим:
\[\frac{ab}{a+b}=b'\left(2.4\right).\]Величины в условиях задачи даны в системе СИ, можем провести вычисления.
\[b'=\frac{2\cdot 1}{2+1}=0,667\left(м\right).\]Ответ: $b'=0,667м.$












