Зависимости показателей преломления и поглощения от частоты

Зависимость показателя преломления от частоты

Для получения зависимости показателя преломления вещества от частоты следует провести анализ механизма поляризации атома (молекулы) в электромагнитном поле волны света.

При распространении волны света сквозь вещество на каждый электрон среды действует сила, которую можно представить как:

где $\alpha \ $-- определяется координатами рассматриваемого электрона, $E_0$ -- амплитуда напряженности электрического поля волны.

Уравнение движения электрона без затухания колебаний имеет вид:

где ${\omega }_0$ -- собственная частота колебаний электрона. Если к правой части выражения (2) добавить слагаемое вида: $-i\frac{q_e}{m}E_0{sin \left(\omega t+\alpha \right)\ }$, то можно перейти к комплексным функциям $\hat{E},\ \hat{r}$, и записать уравнение (2) как:

где ${\hat{E}}_0=E_0e^{i\alpha }$ -- комплексная амплитуда электрического поля световой волны. Решение уравнения (3) ищем в виде:

где ${\hat{r}}_0$ -- комплексная амплитуда колебаний электрона. Подставим выражение (4) в уравнение (3), имеем:

Если выражение (5) умножить на $e^{i\omega t}$, то получим:

Возьмем вещественную часть от выражения (6), получим:

Наведенный полем дипольный момент молекулы совершает колебания по закону:

Используя выражение (8) получим значение поляризуемости молекулы ($\alpha $):

Диэлектрическую проницаемость вещества с полярными молекулами можно выразить как:

где $n_0$ -- концентрация молекул.

Для $k$ -- электронов, имеющих разные собственные частоты ${\omega }_{0k}$ выражение (10) можно записать как:

Зависимость показателя поглощения от частоты

Коэффициент поглощения ($\mu $) -- величина, обратная толщине слоя вещества при распространении сквозь который интенсивность света уменьшается в $e$ раз. Этот коэффициент зависит от длины волны света ($\lambda $) (или частоты $\omega $). То есть на ряду с дисперсией коэффициента преломления существует дисперсия коэффициента поглощения. Для веществ, атомы которых почти не взаимодействуют друг с другом (газы) коэффициент поглощения для множества частот волн почти равен нулю, только для узких областей спектра имеет резкие максимумы. Данные максимумы соответствуют резонансным частотам колебаний электронов внутри атомов. Если молекулы состоят из нескольких атомов, то выявляются частоты, которые соответствуют колебаниям атомов внутри молекул. Массы атомов существенно больше массы электрона, следовательно, молекулярные частоты много меньше атомных. Около каждой собственной часты атома или молекулы коэффициент поглощения резко растет. Измерение коэффициента поглощения единственный метод определения собственных частот атомов, молекул.

В твердых телах или растворах области аномальной дисперсии существенно расширяются и становятся полосами поглощения. Между такими полосами лежат области частот имеющих слабое поглощение. Зависимость коэффициента поглощения от длины волны показана на рис.1

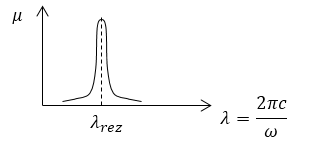
Рисунок 1.

Качественное представление о зависимости коэффициента поглощения от частоты (длины волны) можно получить, если сфотографировать сплошной спектр источника сквозь слой поглощающего вещества. С увеличением коэффициента поглощения отчетливее проявляется ослабление соответствующих участков спектра.

Изменение поглощения в ультрафиолетовой и инфракрасной областях спектра, сейчас используют для определения молекулярного состава сложных смесей. Так, спектры поглощения некоторых органических молекул являются очень характерными, поэтому по ним можно определять молекулярный состав и количественное содержание компонент.