Корреляционная функция
Пусть в точку ($А$), где наблюдаются колебания, две волны приходят в момент времени $t$. Эти колебания испускают источники $S_1$ и $S_2$ в моменты времени $t-{\theta }_1$ и $t-{\theta }_2$, ${\theta }_1$,$\ {\theta }_2$ - время, которое тратится на то, чтобы свет дошел от источников до избранной точки пространства, где рассматриваются колебания. Будем считать, что рассматриваемые колебания стационарны. Исследуемые колебания в точке $А$ обозначим как $E_1(t-{\theta }_1)$ и $E_2(t-{\theta }_2)$. Соответственно, суммарное колебание в точке $А$ можно записать как:
Для того чтобы найти интенсивность колебаний в избранной точке пространства, выражение (1) следует умножить на комплексно сопряженную величину к $E$ и провести усреднение по времени, то есть:
Так как мы рассматриваем стационарные колебания, то в среднем произведение $\overline{E_1\left(t-{\theta }_1\right){E_1}^*\left(t-{\theta }_1\right)}$ не зависит от $t\ и\ {\theta }_1$. Это произведение представляет собой интенсивность $I_1$ первого колебания, которое пришло в точку $А$:
где $\tau$ - размер временного интервала, по которому делается усреднение. Аналогичный вывод делаем по второму слагаемому правой части выражения (2):
где $I_2$ - интенсивность второго колебания.
Выражение $\overline{E_1\left(t-{\theta }_1\right){E_2}^*\left(t-{\theta }_2\right)+{E_1}^*\left(t-{\theta }_1\right)E_2\left(t-{\theta }_2\right)}$ в виду стационарности колебаний не зависит от t, ${\theta }_1$ и ${\theta }_2$ в отдельности, а зависит от $\theta ={\theta }_2-{\theta }_1$. Величина $\theta $ - время запаздывания второго колебания относительно первого. Введем следующее обозначение:
где $F_{12}\left(\theta \right)$ - комплексная функция, которая характеризует степень согласованности колебаний в заданной точке $A$. Эта функция называется корреляционной функцией (взаимной корреляционной функцией) колебаний $E_1\ и\ E_2\ $. В том случае, если колебания исходят от одного источника, но идет в точку $А$ разными путями, при этом функции $E_1(t)\ и\ E_2(t)$ могут быть тождественными. В таком случае $F_{11}\left(\theta \right)=F(\theta )$ называют автокорреляционной функцией.
Нормированная корреляционная функция, ее связь со спектром
Корреляционная функция зависит от интенсивностей суммируемых колебаний:
где $f_{12}\left(\theta \right)$ - нормированная корреляционная функция, зависящая только от времени запаздывания ($\theta $). С помощью нормированной корреляционной функции интенсивность результирующей волны в точке $А$ может быть записана как:
Если рассматриваемые нами волны являются квазимонохроматическими, то есть можно записать:
то найдем корреляционную функцию в соответствии с (5):
Из формулы (9) следует, что $f_{12}$ быстро изменяющаяся функция времени запаздывания $\theta $. Величина (${\gamma }_{12}$) равная:
называется комплексной степенью когерентности колебаний, ее модуль просто степенью когерентности колебаний в точке $А$:
Следовательно, получаем, что:
где ${\gamma }_{12}\left(\theta \right)$ - нормированная взаимная корреляционная функция для амплитуд $a_1\left(t\right)\ и\ a_2\left(t\right).$ Тогда интенсивность света в точке А запишем как:
Положим, что:
тогда в естественной форме выражение (13) представим как:
Величины вещественных амплитуд колебаний ($\left|a_1\right|\ и\ \left|a_2\right|\ $) и соответствующие интенсивности $I_1$ и $I_2$ не зависят от выбора промежуточной частоты ${\omega }_0$ в спектральном интервале $\triangle \omega $ квазимонохроматического света. Не зависит от выбора ${\omega }_0$ полная фаза (${\omega }_0\theta +\delta $). Тогда как добавочная фаза $\delta $ зависит от выбора ${\omega }_0$. Полная фаза определяет наиболее быстрые изменения интенсивности поля света в пространстве, то есть при переходе от одной интерференционной полосы к другой. Функция $\left|{\gamma }_{12}\left(\theta \right)\right|$ при этом изменяется медленно, поэтому при таком переходе ей часто пренебрегают. Получаем, что в максимумах интенсивности $cos\left({\omega }_0\theta +\delta \right)=+1,\ $в минимумах $cos\left({\omega }_0\theta +\delta \right)=-1$. Следовательно:
Видность (V) интерференционных полос можно определить как:
В том случае, если $\left|{\gamma }_{12}\left(\theta \right)\right|=0$, интерференционных полос не получается. Колебания называют некогерентными. Если при этом ${\gamma }_{12}\left(\theta \right)=0$ при любых величинах $\theta $, то мы имеем дело с полной некогерентностью. Когерентность называют полной, если $\left|{\gamma }_{12}\left(\theta \right)\right|=1$ при любом $\theta $. В таком случае интерференционные полосы максимально контрастны. При $0
Связь автокорреляционной функции и спектральной плотности излучения
Соотношение, связывающее автокорреляционную функцию $F(\theta )$ со спектральной плотностью излучения ($I_{\omega }(\omega )$) можно представить как:
Так как мы рассматриваем стационарный поток света, то пределы интегрирования в выражении (19) можно заменить любыми другими не изменяя при этом ширину интервала интегрирования. При этом условии выражение (19) можно записать как:
где $F^*\left(\theta \right)=F\left(-\theta \right)$.
Справедливо обратное соотношение:
Данное соотношение позволяет найти функцию корреляции, используя эмпирические данные спектральной плотности $I_{\omega }\left(\omega \right)$.
Запишите выражение для степени когерентности в случае колебаний, которые представлены как $E\left(t\right)=sin({\omega }_0t)$ в интервале $0
Решение:
Представим заданное колебание в комплексной форме, получим:
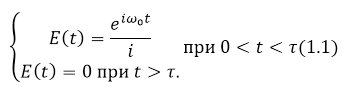
Рисунок 1.
Будем считать, что промежуток, по которому производим усреднение, равен $\tau $. При этом произведение $E\left(t\right)E^*\left(t-\theta \right)\ne 0$ для интервала времени $0 \[\overline{E\left(t\right){E_1}^*\left(t-\theta \right)}=\frac{1}{\tau }\int\limits^{\tau }_0{e^{i{\omega }_0\theta }dt=\frac{\tau -\theta }{\tau }}e^{i{\omega }_0\theta }=F\left(\theta \right)=f\left(\theta \right)(1.2).\]
Получаем, что:
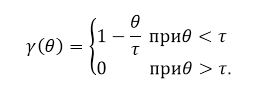
Рисунок 2.
Ответ:
Рисунок 3.
Получите формулу связи функции автокорреляции ($F(\theta )$) и спектральной плотности излучения ($I_{\omega }\left(\omega \right)$).
Решение:
В качестве основы для решения задачи используем определение автокорреляционной функции:
\[F\left(\theta \right)=\overline{E(t)E^*(t-\theta )}=\frac{1}{\tau }\int\limits^{\frac{\tau }{2}}_{-\frac{\tau }{2}}{E(t)E^*(t-\theta)dt(2.1)}.\]Для квазимонохроматических волн можно записать:
\[E=a{(t)e}^{i\omega t},\ E^*=a^*{\left(t\right)e}^{-i\omega t}\left(2.2\right).\]Подставим (2.2) в (2.1), получим:
\[F\left(\theta \right)=\frac{1}{\tau }\int\limits^{\frac{\tau }{2}}_{-\frac{\tau }{2}}{a{(t)e}^{i\omega t}a^*{\left(t\right)e}^{-i\omega (t-\theta )}dt=\frac{1}{\tau }\int\limits^{\frac{\tau }{2}}_{-\frac{\tau }{2}}{{a(t)a}^*{\left(t\right)e}^{i\omega (\theta )}dt}=\frac{2\pi }{\tau }\int\limits^{\infty }_0{a\left(\omega \right)a^*\left(\omega \right)e^{i\omega \theta }d\omega }(2.3)}.\]Где использована формула перехода для амплитуды:
\[a\left(\omega \right)=\frac{1}{2\pi }\int\limits^{\frac{\tau }{2}}_{-\frac{\tau }{2}}{E(t)e^{-i\omega t}dt}.\]Учтем, что спектральная плотность излучения равна:
\[I_{\omega }\left(\omega \right)=\frac{2\pi }{\tau }a\left(\omega \right)a^*\left(\omega \right)\left(2.4\right).\]Получаем в результате:
\[F\left(\theta \right)=\int\limits^{\infty }_0{I_{\omega }\left(\omega \right)}e^{i\omega \theta}d \omega.\]Что и требовалось получить.











