Принцип Гюйгенса
Обосновывая волновую теорию света, Гюйгенс предложил принцип, который позволял наглядно решать некоторые задачи распространения и преломления света. Смысл его в том, что: Если в какой - либо момент времени известен световой волновой фронт, то для того, чтобы определить его положение через некоторый промежуток времени равный $\ \triangle t$, то каждую точку фронта следует рассматривать как источник сферической волны, построить вокруг такого вторичного источника волн сферу, имеющую радиус $c\triangle t$, где $c$ - скорость света в вакууме. При этом поверхность, которая огибает вторичные сферические волны, будет являться фронтом исходной волны через заданный промежуток времени $\triangle t$.
По физическому содержанию принцип Гюйгенса выражает взгляд на свет как непрерывный процесс в пространстве. При использовании принципа Гюйгенса можно объяснить почему, волны света попадают в область геометрической тени.
Основной проблемой принципа Гюйгенса является то, что он не учитывает явления интерференции света. Этот принцип не дает сведений об амплитуде и интенсивности волн.
Принцип Гюйгенса - Френеля, его аналитическое выражение
Френель развил принцип Гюйгенса, и это положение стало формулироваться так: Любая точка, принадлежащая волновому фронту, превращается в источник вторичных волн (это из принципа Гюйгенса), при этом вторичные источники являются когерентными между собой и испускаемые ими вторичные волны интерферируют. Для поверхности, совпадающей с волновой поверхностью, мощности вторичного излучения равных по площади участков одинаковы. Причем свет, распространяющийся от каждого вторичного источника идет в направлении внешней нормали.
Рэлей обобщил вышеназванный принцип:
Окружим все источники света $S_1,S_2,S_3,\dots $ замкнутой поверхностью $(F)$ произвольной формы. При этом любую точку поверхности $F$ можно считать вторичным источником волн, которые распространяются по всем направлениям. Данные волны когерентны, так как возбуждены одними и теми же первичными источниками. Световое поле, которое появляется, как результат их пространственной интерференции, за пределами поверхности $F$ совпадает с полем реальных источников света.
Так, реальные источники света можно заменить светящейся поверхностью, которая их окружает. Причем, по всей этой поверхности как бы непрерывно распределены когерентные вторичные источники световых волн. Отличие этой гипотетической поверхности в том, что она прозрачна относительно любого излучения.
Предположим, что источник света монохроматический, среда однородная и изотропная. Таким образом, в соответствии со скорректированным принципом каждый элемент поверхности волны $S$ (рис.1) является источником вторичной сферической волны, имеющей амплитуду пропорциональную размерам данного элемента ($dS$).
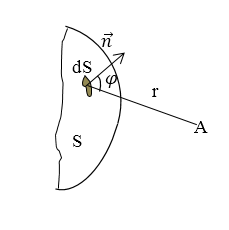
Рисунок 1.
От любого участка $dS$ волновой поверхности в точку $А$ (рис.1), которая находится перед поверхностью $S$, приходит колебание, которое можно описать следующим уравнением:
где $\left(\omega t+{\alpha }_0\right)$ - фаза колебаний в месте нахождения поверхности $S$, $k$ - волновое число, $r$ - расстояние от элемента поверхности ($dS)$ до точки $A$, $a_0$ - амплитуда колебания света в месте нахождения элемента $dS$. $K$ - коэффициент, зависящий от угла $\varphi $ между нормалью $\overrightarrow{n}$ к площадке $dS$ и направлением от нее к точке $4А$. Если $\varphi =0,\ $то мы имеем $K=K_{max}$, при$\ \ \varphi =\frac{\pi }{2}$ $K=0.$
Суммарное колебание в точке А находится как суперпозиция колебаний, которые берутся для всей волновой поверхности $S$, то есть:
Формула (2) является интегральной формулировкой принципа Гюйгенса - Френеля.
Трактовка принципа Гюйгенса - Френеля
Френель искусственное предположение Гюйгенса об огибающей вторичных волн, заменил четким физическим положением, по которому вторичные волны, складываясь, интерферируют. При этом свет виден в максимумах интерференции, там, где волны взаимно гасят друг друга, имеется темнота. Так, объяснен физический смысл огибающей. К огибающей вторичные волны подходят в одинаковых фазах, поэтому интерференция вызывает большую интенсивность света. Принцип Гюйгенса - Френеля поясняет отсутствие обратной волны. Вторичные волны, которые распространяются от волнового фронта вперед, идут в свободное от возмущения пространство. При этом они интерферируют только между собой. Вторичные волны, которые идут назад, попадают в пространство, где уже присутствует прямая волна, так вторичные волны гасят прямую волну, следовательно, после прохождения волны пространство на ней не имеет возмущений.
В формулировке Рэлея рассматриваемый принцип означает, что волна, которая отделилась от своего источника, далее существует автономно, не зависит от присутствия источников.
Принцип Гюйгенса - Френеля позволяет объяснить явление дифракции.
Задание: Запишите выражение для напряженности электрического поля ($E$) в волне, если считать, что волна сферическая и распространяется свободно.
Решение:
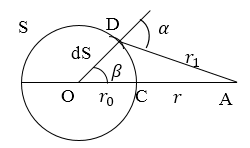
Рисунок 2.
Рассмотрим свободное распространение сферической волны в однородной среде (рис.2), его можно описать, используя уравнение:
\[E_0=A_0\frac{1}{r_0}e^{i\left(\omega t-kr_0\right)}\left(1.1\right).\]Вспомогательной волновой поверхностью в нашем случае является поверхность S, имеющая радиус $r_0$. По утверждению Френеля каждый элемент этой поверхности ($dS$) испускает вторичную сферическую волну. При этом волновое поле, испускаемое элементом $dS$ в точке $А$ найдем как:
\[dE'=a\frac{A_0dS}{r_1}e^{i\left(\omega t-kr_1\right)}\left(1.2\right).\]Используя гипотезу Френеля имеем:
\[a=K\left(\alpha \right)\frac{1}{r_0}e^{i\left(-kr_0\right)}\left(1.3\right),\]где $K\left(\alpha \right)$ - функция, зависящая от длины волны и угла между нормалью к фронту волны и направлением распространения вторичной волны (рис.2).
Полное волновое поле в точке $А$ представим интегралом:
\[E=\int\limits_S{K\left(\alpha \right)\frac{1}{r_0}e^{i\left(-kr_0\right)}}\frac{A_0}{r_1}e^{i\left(\omega t-kr_1\right)}dS=\int\limits_S{A_0K\left(\alpha \right)\frac{1}{r_0r_1}}e^{i\left(\omega t-kr_1-kr_0\right)}dS\left(1.4\right).\]Примем в качестве элемента $dS$ площадь кольца, которое вырезается из волнового фронта двумя бесконечно близкими концентрическими сферами центры которых находятся в точке $А$ (рис.2). В таком случае, можно записать, что:
\[dS=2\pi {r_0}^2sin\beta d\beta \left(1.5\right).\]В качестве переменной интегрирования примем расстояние $r_1.$ Величины $r_0$ и $r$ считаем постоянными. Из треугольника $DOA$ найдем:
\[{r_1}^2={r_0}^2+{\left(r_0+r\right)}^2-2r_0\left(r_0+r\right)cos\beta \left(1.6\right).\]Продифференцируем выражение (1.6), имеем:
\[2r_1dr_1=2r_0\left(r_0+r\right)sin\beta d\beta \to sin\beta d\beta =\frac{2r_1dr_1}{2r_0\left(r_0+r\right)}\to dS=\pi r_0\frac{2r_1dr_1}{\left(r_0+r\right)}\left(1.7\right).\]Подставим выражение (1.7) для $dS$ в формулу (1.4), получим:
\[E=\int\limits^{r_{max}}_r{A_0K\left(r_1\right)\frac{1}{r_0r_1}}e^{i\left(\omega t-kr_1-kr_0\right)}\pi r_0\frac{2r_1dr_1}{\left(r_0+r\right)}=\frac{2\pi A_0}{\left(r_0+r\right)}e^{i\left(\omega t-kr_0\right)}\int\limits^{r_{max}}_r{K\left(r_1\right)e^{-ikr_1}}dr_1\left(1.8\right),\]где функцию $K\left(\alpha \right)\ \ рассматриваем\ как$ функцию $r_1$. При этом $r_{max}=r+2r_0.$
Ответ: $E=\frac{2\pi A_0}{\left(r_0+r\right)}e^{i\left(\omega t-kr_0\right)}\int\limits^{r_{max}}_r{K\left(r_1\right)e^{-ikr_1}}dr_1.$
Задание: Как используя принцип Гюйгенса - Френеля объяснить явление дифракции?
Решение:
Допустим, что плоская волна падает на экран перпендикулярно отверстию в нем. Согласно принципу Гюйгенса - Френеля каждая точка участка, волнового фронта, который выделяется отверстием в экране, становится источником вторичных волн. Если среда является однородной и изотропной вторичные волны являются сферическими. При построении огибающей вторичных волн для фиксированного момента времени получится, что фронт волы заходит в область геометрической тени, что означает, что волна огибает отверстие.











