Использование векторных диаграмм существенно упрощает расчёты и их объяснение в оптике. Так, принцип Гюйгенса - Френеля можно представить в наглядной форме в виде векторной диаграммы (рис.1). На этой диаграмме результирующая амплитуда вектора напряжённости поля волны $\overrightarrow{E_m}$ представляется как векторная сумма амплитуд $\left(d\overrightarrow{E_1},d\overrightarrow{E_2,\ }\dots ,\ d\overrightarrow{E_n\ }\right)\ $колебаний некоторой избранной точке пространства, создают разные элементы $dS$ светящейся поверхности $S$ с учетом их фаз (углов между ними).
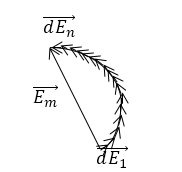
Рисунок 1.
Спираль Френеля
Попытаемся решить задачу о распространении света от источника $S$ к точке $A$ графическим методом (методом сложения амплитуд). Проведем разбиение волновой поверхности на кольцевые зоны (подзоны) (аналоги зон Френеля), только пусть они будут меньше по ширине, при этом пусть разность хода от краев зоны до точки $A$ равна малую долю длины волны ($\lambda $), их равно $n$. Вектором, длина которого равна амплитуде колебаний, отобразим колебание, которое создает в точке $A$ каждая зона. Угол, который образует данный вектор с направлением, которое приняли за начало отсчета, является начальной фазой колебаний. Амплитуда данных колебаний является медленной убывающей, при переходе от зоны к зоне. Между началом и концом зоны фаза изменяется на величину:
Аналитически сложение амплитуд запишется как:
где $E_0$ - амплитуда волны, которая приходит в точку $A$ от каждой подзоны. При этом будем считать, что фаза волны от нулевого участка ($М_0$) равна нулю. Аналитическое сложение амплитуд можно сделать графически (рис.2). Если число подзон увеличить до $n\to \infty $, то ломаная кривая (рис.2) превращается в плавную кривую (рис.3). При этом длина отрезка $\left|M_0P\right|$ пропорциональна амплитуде волны в точке $A$, в том случае если открыта часть нулевой зоны от центра до границы, которая соответствует точке $P$. Длина отрезка $\left|M_0M_1\right|$ пропорциональна амплитуде при полном открытии нулевой зоны. Графическое построение амплитуды, если учитывать вклад от других зон ведется по аналогии. При этом следует учесть, что величина $E_0$ с увеличением расстояния от точки уменьшается. Вследствие чего непрерывная кривая имеет вид спирали (рис.4). Эта спираль (спираль Френеля) дает возможность найти амплитуду при открытии любого числа зон (их частей).
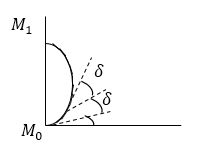
Рисунок 2.
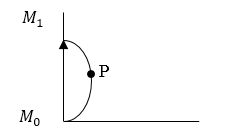
Рисунок 3.
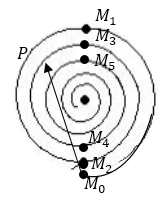
Рисунок 4.
Длина отрезка $\left|M_0P\right|$ (рис.4) пропорциональна величине амплитуды при открытии нулевой, первой, второй и части третьей зоны. Величины отрезков $\left|M_0M_1\right|$, $\left|M_0M_2\right|$, ... пропорциональны амплитудам при открытии нулевой зоны, нулевой и первой зоны соответственно. В том случае, если открыты все зоны, то амплитуда пропорциональна:
что показывает - при открывании одной нулевой зоны амплитуды волн в точке $A$ в два раза (примерно) больше, интенсивность соответственно в четыре раза больше, чем когда открыты все зоны. Если открыты нулевая и первая зоны, то амплитуда пропорциональна $\left|M_0M_2\right|$, следовательно, интенсивность мала. Интенсивность, падающей световой волны в точке $A$ при увеличении радиуса отверстия (непрерывном) непрерывно меняется. Используя спираль (рис.4) можно изобразить график зависимости амплитуды волны от радиуса отверстия ($r$) .
Спираль Френеля получают, когда на отверстие падает сферическая волна конечного радиуса. Она состоит из элементарных векторов, которые представляют колебания от элементов фронта волны. Вся спираль - это колебания полностью открытого фронта, в том случае, если открывают часть фронта, то мы имеем часть спирали Френеля. Амплитуда результирующих колебаний связывается с длиной вектора, который соединяет начало и конец спирали.
Задание: Радиус круглого отверстия, на которое падает световая волна, равен половине первой зоны Френеля, радиусу первой зоны Френеля, радиусу второй зоны Френеля. Чему равны результирующие интенсивности падающей волны, которая прошла через отверстие для трех означенных случаев?
Решение:
Допустим, что витки спирали Френеля имеют вид окружностей. Амплитуда результирующих колебаний - длина вектора, который соединяет начало спираль и ее конец. Изобразим на рисунке случай, когда открыта половина первой зоны (рис.5).
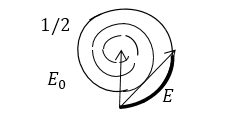
Рисунок 5.
Из рис. 5 очевидно, что:
\[E^{0,5}\approx \sqrt{2}E_0\left(1.1\right).\]Изобразим спираль Френеля для случая, когда радиус отверстия равен первой зоне Френеля (рис.6):
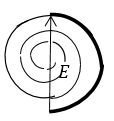
Рисунок 6.
В данном случае амплитуда колебаний равна:
\[E^1\approx 2E_0\left(1.2\right).\]В случае если радиус отверстия равен радиусу второй зоны, то в соответствии с рис.7 получим:
\[E^2\approx 0\ \left(1.3\right).\]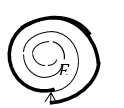
Рисунок 7.
Ответ: $E^{0,5}\approx \sqrt{2}E_0,\ E^1\approx 2E_0,E^2\approx 0\ .$
Задание: Объясните, используя метод векторных диаграмм, что происходит при суммировании амплитуд колебаний для зон Френеля.
Решение:
Если суммировать колебания первой, второй, третьей и т.д. зон Френеля мы получаем (рис.8):
\[E^1\approx 2E_0,\ -E^2\le 2E_0,\ -E^3\le 2E_0\dots \left(2.1\right).\]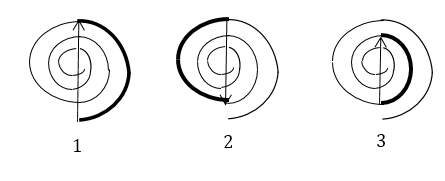
Рисунок 8.
Если складывать колебания только четных (или только нечетных) зон Френеля, то получаются колебания, амплитуда которых существенно больше $E_0$. Так как мы складывали бы значения амплитуд одного знака.











