Поляризация рассеянного света
При возникновении рассеянного естественного света в замутненном веществе зависимость интенсивности рассеянного света от угла рассеяния можно представить как:
где $I_0$ -- интенсивность света, который рассеян под углом $\varphi =\frac{\pi }{2}$ к направлению распространения первичного пучка света. В случае, при котором молекулы, выступающие центрами рассеивания, являются изотропными, то рассеиваемый свет становится частично поляризованным. Только под углом $\varphi =\frac{\pi }{2}$ он оказывается полностью поляризованным. В таком случае плоскость его поляризации, то есть плоскость, в которой совершает колебания вектор $\overrightarrow{E},$ перпендикулярна направлению первичного пучка света.
Если частицы (рассеивающие центры) много меньше длины волны света, то при рассевании происходит поляризация. Рассеиваемый пучок порождает в частицах колебания зарядов. Направления данных колебаний лежат в плоскости, которая перпендикулярна к пучку. При этом колебания вектора напряженности электрического поля во вторичной волне идут в плоскости, которая проходит через направление колебания зарядов. Следовательно, свет, который рассеивают частицы в направлениях нормальных к лучу, будет полностью поляризован (рис.1).
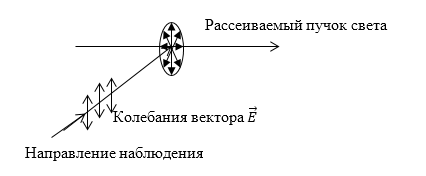
Рисунок 1.
В случае, при котором размер неоднородностей можно сравнить с длинной волны света, электроны в разных точках неоднородностей совершают несинфазные колебания, что существенно усложняет явление рассеяния. Закон Рэлея при этом не выполняется. Интенсивность рассеянного света становится пропорциональна квадрату частоты:
При этом свет, рассеиваемый под углом $\varphi =\frac{\pi }{2}$, является частично поляризованным.
В случае, при котором размер неоднородностей существенно больше длины волны света, то спектральный состав рассеянного света почти совпадает со спектральным составом первичного пучка.
Спектральный состав рассеянного света
Теория спектрального состава рассеянного света на сегодняшний момент хорошо проработана. В том случае, если рассеянию подвергается строго монохроматический свет, то в спектре рассеянного света кроме несмещенной спектральной линии появляются новые линии, имеющие частоты, равные суммам или разностям частот падающего света ($\nu $) и частот собственных колебаний молекул (${\nu }_i$) рассеивающей среды. Такое рассеяние было названо комбинационным.
Линии в спектре комбинационного рассеяния имеющие частоты меньше, чем частота падающего света называют стоксовыми (красными) спутниками, линии имеющие частоты больше частоты падающего света носят название антистоксовых (фиолетовых) спутников. Анализируя спектры рассеяния, делают следующие выводы:
-
линии спутников расположены симметрично по обеим сторонам от несмещенной линии,
-
частоты ${\nu }_i$не зависят от частоты падающего света. Они определены только особенностями рассеивающего вещества, то есть они характеризуют его состав и структуру,
-
количество спутников определено рассеивающим веществом,
-
интенсивность антистоксовых спутников меньше, чем интенсивность стоксовых спутников. Интенсивность антистоксовых спутников с ростом температуры рассеивающей среды увеличивается, для стоксовых спутников интенсивность от температуры почти не зависит.
Законы комбинационного рассеяния получили объяснение в квантовой теории. Рассеяние света рассматривается как процесс, в котором один фотон поглощается молекулой и один испускается. В том случае, если энергии таких фотонов равны, то в рассеянном свете наблюдают несмещенную линию. Если таковые энергии фотонов различны, то молекула переходит из нормального состояния в возбужденное или из возбужденного состояния в нормальное. Так, рассеяние света сопровождают переходы молекул между разными колебательными уровнями, как результат появляется совокупность симметрично расположенных спутников. Количество спутников определено энергетическим спектром молекул. Количество возбужденных молекул меньше, чем находящихся в нормальном состоянии, поэтому интенсивность антистоксовых спутников меньше. При увеличении температуры количество молекул в состоянии возбуждения увеличивается, как следствие, растет интенсивность антистоксовых спутников.
Молекулярные спектры используют при исследованиях строения молекул в спектральном анализе, лазерной спектроскопии, квантовой электронике.
Спектры молекулярного рассеянного света применяют для изучения поверхностных рэлеевских волн, которые распространяются по поверхности границы двух сред и вызваны шероховатостью поверхности раздела. Спектры молекулярного рассеяния позволяют определять скорость звука с частотой порядка ${10}^{10}Гц.$
Особый интерес вызывает изучение спектра молекулярного рассеяния в бинарных растворах, в которых имеется замкнутая область расслаивания, если добавляется третья компонента.
Объясните, почему рассеянный свет поляризован частично, если плоско поляризованная волна света падает на вещество с анизотропными молекулами.
Решение:
Пусть молекулы газа (среды) анизотропны. Падающий свет плоско поляризован, рассеянный свет будет поляризован частично. Данная деполяризация рассеянного света вызвана анизотропией молекул. Допустим, что световой вектор падающей волны ($\overrightarrow{E}$) направлен по оси X. Если молекула обладает сферической симметрией (изотропная), то ее дипольный момент можно определить как:
\[\overrightarrow{p}=\beta \overrightarrow{E}\left(1.1\right),\]то есть дипольный момент сонаправлен с вектором $\overrightarrow{E}.$ В таком случае свет, рассеянный молекулой будет поляризован линейно, с плоскостью колебаний, которая проходит через ось диполя и линию наблюдения. В случае если вещество состоит из изотропных молекул, то векторы $\overrightarrow{p}$ и $\overrightarrow{E}$ не параллельны. Возникнут составляющие вектора $\overrightarrow{p}$ по осям Y и Z. При тепловом движении молекул ориентация молекулы в пространстве постоянно и хаотично изменяется, то поляризуемости молекул по осям координат будут иметь флуктуации. Компоненты $p_y\ и\ p_z$ порождают рассеянные волны с поляризацией, отличающейся от поляризации излучения, которое дает $p_x$. Что ведет к деполяризации рассеянного света.
Если волна света плоско поляризована и рассеивается на веществе, состоящем из изотропных молекул, какой поляризацией будет обладать рассеянная волна.
Решение:
Пусть падающая волна линейно поляризована, тогда векторы поля волны ($\overrightarrow{E}$) и дипольный момент молекулы ($\overrightarrow{p}$) параллельны одному постоянному направлению. Электрическое поле диполя на больших расстояниях от него (в зоне волны) определено формулой:
\[E_{иe}=cB_{\varphi }=-\frac{1}{4\pi {\varepsilon }_0}\frac{{\omega }^2}{c^2}\frac{{sin \left(\theta \right)\ }}{r}p\left(t-\frac{r}{v}\right),\ E_r=E_{\varphi }=0,\ B_r=B_{\varphi }=0\left(2.1\right),\]где $\varphi $ -- полярный и аксиальный углы, $r-$расстояние от диполя до точки, в которой определяется поле, $v=\frac{c}{n}$ -- скорость света в исследуемой среде. $\theta $- угол между осью диполя и направлением рассеянного излучения. Рассеянный свет плоско поляризован, при этом электрический вектор лежит в плоскости, которая проходит через ось диполя и направление излучения.












