Опыты по поляризации света
Явление поляризации возникает при отражении и преломлении света на границе двух изотропных диэлектриков. Данный способ создания поляризованных волн был обнаружен Малюсом. Ученый обнаружил, что при вращении кристалла вокруг луча, который был отражен от стекла, интенсивность света периодически изменяется. Он сделал вывод о том, что отражение света от стекла подобно прохождению им через турмалин (относительно возникновения поляризации). В данных опытах полного погасания света обнаружено не было, проявилось только ослабление и усиление его интенсивности.
Допустим, что параллельный пучок неполяризованного света (рис.1) падает на зеркало $S_1S_1$, которое укреплено на оси $O$ с помощью шарнира. В подобном устройстве можно при любом угле падения направить ось $O$ по отраженному лучу, обеспечив возможность вращения вокруг него зеркала. Отраженный свет в этих условиях изучается при помощи пластинки турмалина ($T_2$), которая может поворачиваться вокруг отраженного луча. Наблюдатель при повороте пластинки $T_2$ видит ослабление и усиление света.
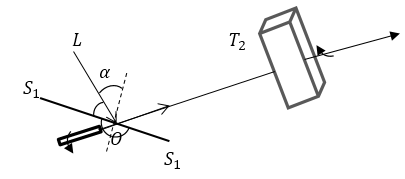
Рисунок 1.
В таком опыте интенсивность света минимальна, когда плоскость, которая проходит через ось кристалла турмалина, параллельна плоскости падения на зеркало. Свет имеем максимальную интенсивность в случае, когда $\ пластинка\ T_2\ $повернута на $90^\circ$. Поляризация света в таком эксперименте оказывается частичной, то есть отраженный луч является смесью естественного и поляризованного света.
Закон Брюстера
Меняя угол наклона зеркала $S_1S_1$ по отношению к лучу, можно убедиться, что доля поляризованного света зависит от угла падения $\alpha $. Если угол растет, увеличивается доля поляризованного света, при определенном его значении отраженный свет становится полностью поляризованным. Величина такого угла (полной поляризации) связана с относительным показателем преломления диэлектрика. В соответствии с законом, который установил Брюстер в 1815 г.:
где ${\alpha }_b$ называют углом Брюстера, отраженный луч является плоско поляризованным, $n_{12}$- показатель преломления второй среды относительно первой.
Если угол падения волны увеличивать дальше, то поляризованность света вновь уменьшается. При падении волны под углом полной поляризации луч отраженный и преломленный составляют прямой угол.
Эксперименты показывают, что электрический вектор в отраженном поляризованном свете совершает колебания перпендикулярно плоскости падения. При неполной поляризации данное направление колебаний становится преимущественным.
При анализе преломленного света получают, что он тоже частично поляризован. Выделенное направление колебаний электрического вектора при этом находится в плоскости падения луча. Если соединить отраженный и преломленный свет, то получается первичный неполяризованный свет. Значит, прозрачная пластина диэлектрика сортирует лучи неполяризованного света, отражает преимущественно лучи с одним направлением колебаний и пропускает перпендикулярные колебания. Размер части поляризованного света в преломленном пучке зависит от угла падения света и показателя преломления вещества.
Если угол падения света равен углу Брюстера, то поляризация является максимальной, но не полной. Можно повысить степень поляризации преломленных, частично поляризованных лучей, если подвергнуть из следующим преломлениям. Так, при падении под углом Брюстера на совокупность из $8-10$ пластинок (стопа Столетова), преломленный и отраженные пучки света почти полностью становятся поляризованными. Интенсивность отраженного и прошедшего пучков света равны и равны $0,5$ интенсивности падающего света при отсутствии поглощения. Направления колебаний световых векторов в отраженном и преломленном пучках взаимно перпендикулярны.
Задание: Покажите, что если пучок света падает на границу раздела двух веществ под углом Брюстера, то отраженный и преломленный пучки света перпендикулярны друг другу.
Решение:
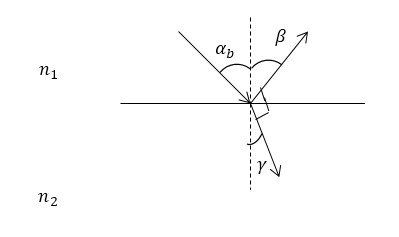
Рисунок 2.
За основу решения задачи возьмем закон Брюстера:
\[tg{\alpha }_b=n_{12}\left(1.1\right)и\ \]закон преломления:
\[\frac{sin ({\alpha }_b)}{sin (\gamma )}=n_{12}\left(1.2\right).\]Зная, что:
\[tg\left({\alpha }_b\right)=\frac{{sin \left({\alpha }_b\right)\ }}{{cos \left({\alpha }_b\right)\ }}\left(1.3\right).\]Сравнивая формулы (1.3),(1.2) и (1.1) видим, что:
\[tg{\alpha }_b=\frac{{sin \left(\alpha_b\right)\ }}{{cos \left(\alpha_b\right)\ }}=\frac{{sin \left(\alpha_b\right)\ }}{{sin \left(\gamma \right)\ }}\left(1.4\right).\]Из выражения (1.4) очевидно, что:
\[{cos \left(\alpha_b\right)\ }={sin \left(\gamma \right)\ }\left(1.5\right).\]Из формулы (1.5) имеем:
\[{\alpha }_b+\gamma =\frac{\pi}{2}\left(1.6\right).\]Из закона отражения помним, что:
\[{\alpha }_b=\beta \left(1.7\right).\]Подставим (1.7) в (1.6):
\[\beta +\gamma =\frac{\pi }{2}(1.8).\]Из выражения (1.8) следует, что между отраженным и преломленным лучом в данном случае угол $90^\circ$.
Что требовалось показать.
Задание: Каким должен быть угол к горизонту для Солнца ($\varphi $), чтобы его лучи, которые отражаются от поверхности воды в водоеме, были максимально поляризованы? Показатель преломления воды в водоеме можно считать равным $n=1,33$.
Решение:
В качестве основы для решения задачи используем закон Брюстера:
\[tg{\alpha }_b=n_{12}\left(2.1\right).\]Так как показатель преломления воздуха будем считать равным единице, то можно записать: $n_{12}=n$. Из уравнения (2.1) выразим угол падения лучей, при котором они могут быть максимально поляризованы (угол Брюстера) при отражении:
\[{\alpha }_b=arctg\left(n\right)\left(2.2\right).\]В таком случае, угол к горизонту под которым должно находиться Солнце для максимальной поляризации отраженных лучей будет равен:
\[\varphi =\frac{\pi }{2}-{\alpha }_b=\frac{\pi }{2}-arctg\left(n\right).\]Проведем вычисления:
\[\varphi =90{}^\circ -arctg\left(1,33\right)=36,9{}^\circ \]Ответ: $\varphi =36,9{}^\circ $.











