Нормальная дисперсия
Выражение, связывающее показатель преломления среды, с частотой падающего на вещество света $\omega :$
где $n_0$ -- концентрация молекул, объясняет явление дисперсии. Данная формула справедлива практически только для газов, так как она получается без учета взаимодействия между атомами (молекулами) и учитывает только действие внешнего поля на электронное облако молекулы. То есть можно сделать вывод, что данный закон выполняется только для разреженных газов. Однако следует отметить, что для качественного объяснения механизма дисперсии эту формулу (1) можно использовать для жидкостей и газов.
Если показатель преломления близок к единице (для разреженных газов), то можно записать:
В таком случае выражение (1) можно упростить и записать как:
При этом график зависимости $n(\omega )$ называют дисперсионной кривой. На (рис.1) штриховыми линиями изображен график, который определяется выражением (3).
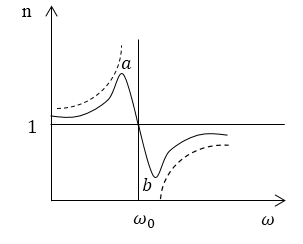
Рисунок 1.
Из рис.1 видно, что в том случае, если частота колебаний поля в волне ($\omega $) меньше собственной частоты колебаний электрона (${\omega }_0$), то есть $\omega 1$). При $\omega \to {\omega }_0$ $n\to \infty .$ Если частота колебаний поля в волне света больше, чем собственная частота колебаний оптического электрона ($\omega >{\omega }_0$), то $n
В том случае, если показатель преломления растет с увеличением частоты, то такая дисперсия называется нормальной. Нормальная дисперсия наблюдается во всех прозрачных областях.
Для частот, которые малы ($\omega \ll {\omega u}_0)$ выражение (3) превращается в:
В соответствии с (4) значения показателя преломления $n$ статичны и могут сильно отличаться от величин показателей преломления для оптических частот.
В том случае, если частота колебаний поля в световой волне удовлетворяет условию ($\omega \gg {\omega }_0$), то показатель преломления стремится к единице в соответствии с выражением:
но остается меньше ее. Получается, что для излучения с коротким диапазоном волн диэлектрик оптически менее плотная среда, чем вакуум. В этом случае может происходить полное отражение от поверхности вещества. Из формулы (6) следует, что при очень больших частотах характер связи электронов в атомах роли не играет. При этом коэффициент преломления зависит от суммарного количества оптических электронов в единице объема, совершающих колебания.
Аномальная дисперсия
Если принимать во внимание затухание ($коэффициент\ \gamma \ne 0$), то кривая дисперсии в окрестностях точки ${\omega }_0$ становится непрерывной и не уходит в бесконечность при ${\omega }_0=\omega .$ Представим показатель преломления в комплексном виде ($\hat{n}$):
где $n$ -- действительная часть показателя преломления, $\xi $ -- мнимая часть показателя преломления. Для $\hat{n}$ имеем выражение:
В случае, когда модуль $\hat{n}$ мало отличается от единицы, то можно записать:
Из выражения (8) следует:
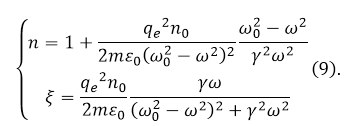
Рисунок 2.
Кривая дисперсии около резонансной частоты ($\omega ={\omega }_0$) представлена отрезком $ab$ сплошной кривой на рис.1. Около резонансной частоты $n$ с увеличением частоты уменьшается. Это явление носит название аномальной дисперсии.
Задание: Как связаны между собой полосы поглощения света веществом и области дисперсии?
Решение:
Явление аномальной дисперсии тесно связано с поглощением света. Все вещества, имеющие аномальную дисперсию, интенсивно поглощают свет в этой области. При этом около полосы поглощения показатель $n$ изменяется с высокой скоростью. Его значения со стороны более длинных волн выше, чем со стороны коротких. Любое вещество имеет свои полосы поглощения, и общий ход $n$ вызван распределением этих полос по спектру. Следовательно, противопоставление понятий нормальной и аномальной дисперсии не имеет смысла. Если рассматривать полную дисперсионную картину любого вещества, то в ней имеется аномальная и нормальная дисперсии, соответственно, полосы поглощения и области, расположенные между ними.
Задание: В чем состоит суть, предложенного Д.С. Рождественским метода крюков?
Решение:
Д.С. Рождественский предложил метод измерения дисперсии около полосы поглощения. Он использовал возможность изменения наклона интерференционных полос при введении, в какое - либо плечо, слоя вещества. Ученый разместил в одном плече слой изучаемого вещества, а в другой - стеклянную пластину. В исследуемом веществе около полосы поглощения дисперсия изменяется существенно (явление аномальной дисперсии), при этом, найдется такая длина волны, для которой действие исследуемого вещества полностью компенсируется действием стеклянной пластинки, в таком случае наклон кривой интерференции пройдет через ноль. Причем, слева от данного значения длины волны кривые опускаются, справа -- поднимаются (или наоборот), то есть появляется крюк. Местоположение вершины этого крюка в шкале длин волн можно измерить с достаточной точностью.
По положению вершины крюка Рождественский определял $\frac{dn}{d\lambda }$, то есть дисперсию исследуемого вещества при значении длины волны света, которое соответствует точке излома полосы интерференции. Изменяя толщину стеклянной пластины можно менять положение вершины крюка по шкале длин волн, проводя исследование дисперсии в нужном диапазоне длин волн.











