Многоуровневые системы
В квантовой теории динамические системы описываются существенно сложнее, чем в классической физике. Так, одномерный гармонический осциллятор в классической механике полностью определен амплитудой, частотой и начальной фазой колебаний. Тогда как в квантовой механике гармонический осциллятор -- многоуровневая система. Ее полное описание требует бесконечное количество параметров (амплитуд, фаз, которые относят к каждому уровню). Динамика подобной системы определена как сумма всех состояний. В квантовой теории поля устанавливают параллель между монохроматической волной и гармоническим осциллятором. При этом волна описывается суммой состояний поля.
Взаимодействие многоуровневой квантовой системы с переменным внешним электромагнитным полем, если частота поля находится около частоты переходов системы между двумя стационарными состояниями, при этом амплитуда невелика, описывается упрощенной моделью. В такой модели можно получить приближенные аналитические зависимости амплитуд и вероятностей разрешенных квантовых переходов от параметров вешнего поля, времени его воздействия и параметров, которые характеризуют невозмущенную систему. Такой способ управления квантовой системой является резонансным. При этом наблюдаются однофотонные переходы.
В пределе сильных полей (интенсивность и амплитуда электромагнитного поля велики по сравнению с расстояниями между уровнями в системе) кроме однофотонных переходов, значимую роль играют много фотонные процессы (много фотонное возбуждение, многофотонное рассеяние света и т.д.). Если поля считают сильными, то нельзя говорить о переходах между стационарными уровнями. Данные уровни изменяются и могут двигаться под воздействием импульса накачки. Говорят, что многофотонные резонансы текут при перебросах между квазиэнергетическими уровнями.
Гамильтонианы многоуровневых систем
Поведение многоуровневой системы можно описать, используя матрицы гамильтониана. Пусть система образована двумя линейными независимыми состояниями:
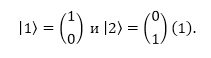
Рисунок 1.
В общем случае состояние будет нормализованной линейной комбинацией:
где ${\left|a\right|}^2+{\left|b\right|}^2=1.\ $ Собственные векторы состояний и собственные значения оператора $\hat{H}$ связаны стационарным уравнением Шредингера:
Изменение состояния во времени задано уравнением Шредингера вида:
Задание: Пусть система в начальный момент времени ($t=0$) находится в состоянии $\left|\left.1\right\rangle \right.=\left(\genfrac{}{}{0pt}{}{1}{0}\right)$. Каково состояние данной системы в момент времени $t$?
Решение:
Пусть гамильтониан системы имеет вид:
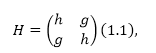
Рисунок 2.
где $g$ и $h$ -- вещественные постоянные. Используем стационарное уравнение Шредингера для того, чтобы найти собственные значения:
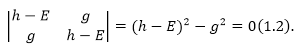
Рисунок 3.
Из уравнения (1.2) следует, что:
\[E_{\pm }=h\pm g\ \left(1.3\right).\]Мы получили, что допустимые уровни энергии:
\[h+g\ и\ h-g\ \left(1.4\right).\]Найдем собственные векторы, для этого матрицу $\hat{H}$ умножаем на найденный вектор, который запишем в общем виде как ($\alpha ,\beta $):
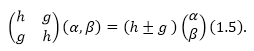
Рисунок 4.
Из выражения (1.5) получаем:
\[h\alpha +g\beta =\left(h\pm g\ \right)\alpha \to \beta =\pm \alpha \left(1.6\right).\]При этом нормализованные векторы запишем в виде:
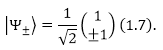
Рисунок 5.
Используя полученные выражения (1.7) запишем начальное состояние как линейную комбинацию состояний собственных векторов оператора Гамильтона:
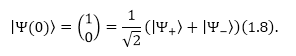
Рисунок 6.
Запишем искомую функцию как:
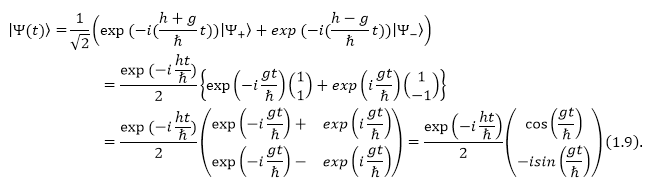
Рисунок 7.
Ответ: В том случае, если при $t=0$ система находилась в состоянии $\left|\left.1\right\rangle \right.$ и при этом гамильтониан имеет отличные от нуля элементы вне диагонали (у нас $g$), то вероятность нахождения системы в каком - то состоянии, носит периодический характер, так как она через некоторый промежуток времени окажется в состоянии $\left|\left.2\right\rangle \right.=\left(\genfrac{}{}{0pt}{}{0}{1}\right)$, а потом вернется обратно.
Задание: 1)Запишите функцию эволюции двухуровневой системы $\left|\left.\Psi(t)\right\rangle \right.$, если собственные состояния этой системы удовлетворяют уравнениям: $H_0\left|\left.1\right\rangle \right.=\hbar {\omega }_1\left|\left.1\right\rangle \right.{\ \ и\ \ H}_0\left|\left.2\right\rangle \right.=\hbar {\omega }_1\left|\left.2\right\rangle \right..$
2)Как изменится гамильтониан системы, если включить внешнее потенциальное поле вида:
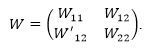
Рисунок 8.
Решение:
Допустим, что у нас имеется двухуровневая система. Собственные состояния этой системы удовлетворяют уравнениям:
\[H_0\left|\left.1\right\rangle \right.=\hbar {\omega }_1\left|\left.1\right\rangle \right.\left(2.1\right),\] \[H_0\left|\left.2\right\rangle \right.=\hbar {\omega }_1\left|\left.2\right\rangle \right.\left(2.2\right).\]Совокупный гамильтониан заданной системы ($H_0$) в базисе $\left(\left|\left.1\right\rangle \right.,\left|\left.2\right\rangle \right.\right)$ можно представить в матричном виде как:
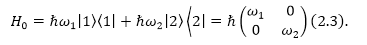
Рисунок 9.
Запишем искомую эволюцию системы:
\[\left|\left.\Psi(t)\right\rangle =\right.\left|\left.1\right\rangle \right.{exp \left(-i{\omega }_1t\right)\ }\left\langle \left.1\right|\right.\left|\left.\Psi\left(0\right)\right\rangle \right.+\left|\left.2\right\rangle \right.{exp \left(-i{\omega }_1t\right)\ }\left\langle \left.2\right|\right.\left|\left.\Psi\left(0\right)\right\rangle \right.\left(2.4\right).\]Допустим, что в гамильтониан внесены изменения, включив внешнее поле. В таком случае:
\[H=H_0+W\left(2.5\right),\]где оператор потенциального поля имеет вид:
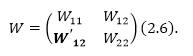
Рисунок 10.
Тогда выражение (2.5) можно переписать как:
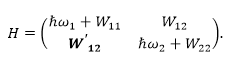
Рисунок 11.
Ответ: 1) $\left|\left.\Psi\left(t\right)\right\rangle =\right.\left|\left.1\right\rangle \right.{exp \left(-i{\omega }_1t\right)\ }\left\langle \left.1\right|\right.\left|\left.\Psi\left(0\right)\right\rangle \right.+\left|\left.2\right\rangle \right.{exp \left(-i{\omega }_1t\right)\ }\left\langle \left.2\right|\right.\left|\left.\Psi\left(0\right)\right\rangle \right..\ $
2)
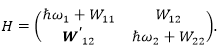
Рисунок 12.












