
Если следовать атомистическим представлениям, то любое вещество надо рассматривать как вакуум, в котором помещены атомы вещества. При падении волны и излучении соседних атомов внутри каждого атома возбуждаются колебания электронов и ядер атомов. Так атомы становятся источниками вторичных сферических волн, которые распространяются между этими ними со скоростью света в вакууме. Данные волны являются когерентными, так как они возбуждены одной падающей волной. Интерференция этих волн между собой и с падающей волной определяет волновое поле во всем пространстве. Так, отраженная волна появляется как результат интерференции вторичных волн, которые выходят из среды в вакуум.
Объяснение отличия фазовой скорости волны при распространении ее в веществе от скорости в вакууме
В теории отражения и преломления основной интерес представляет фазовая скорость, именно она определяет показатель преломления среды. Отличие фазовой скорости от скорости света в вакууме можно объяснить тем, что в каждую точку пространства вторичные волны идут не только от атомов, которые расположены вдоль луча, проходящего через точку наблюдения, но и от других атомов, вне этого луча.
Будем считать атомы материальными точками. В поле волны света атомы имеют переменные во времени дипольные моменты и являются излучателями типа точечных диполей Герца. Поле излучения в волновой зоне определено перпендикулярной составляющей дипольного момента ($p_{\bot }$) к направлению излучения.
Пусть в вакууме по оси $X$ распространяется плоская монохроматическая волна вида:
На пути этой волны перпендикулярно к оси $X$ расположен очень тонкий плоскопараллельный слой (толщина его $\ d\xi $), который состоит из неподвижных атомов, распределенных равномерно по объему слоя (рис.1).
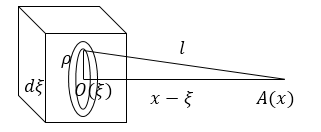
Рисунок 1.
Определим, каково влияние выделенного слоя на фазу колебаний в точке наблюдения ($A(x))$, которая существенно удалена от слоя. Дипольные моменты атомов слоя, находящиеся в возбужденном состоянии из-за падения на них волны можно представить как:
где $\xi $ -- абсцисса слоя. Будем считать, что точка наблюдения находится в волновой зоне диполей слоя. В таком случае электрическое поле каждого диполя в точке $A$ равно:
где $r$ -- расстояние от диполя. Эти выражения требуется суммировать по всем диполям слоя. Используем с этой целью метод кольцевых зон Френеля. Тогда, результирующая напряженность ($d\overrightarrow{E_1}$) всех диполей слоя в точке наблюдения равна одной второй напряженности поля, которое возбуждается в этой же точке диполями только центральной зоны. Значит необходимо суммировать выражение (3) по всем диполям центральной зоны и разделить на два (заменим интегрированием). Вторичные волны, которые исходят от края центральной зоны отстают по фазе на $\pi $ от волны, которая исходит от центра $O$, а значит от падающей волны. Такое отставание по фазе является промежуточным. Так появляется замедление скорости распространения фазу волны, если она идет через вещество.
Выделим кольцо (рис.1) внутренний радиус которого равен $\rho $, наружный $\rho +d\rho $. В элементе объема $dV=2\pi \rho \cdot d\rho \cdot d\xi $ находится $NdV$ диполей и их число велико ($N$ - количество диполей в единице объема). Учитываем все сказанное выше, кроме того:
В качестве переменной величины примем расстояние $r$. В рамках центральной зоны величину $\overrightarrow{p_{0\bot }}$ считаем постоянной и равной $\overrightarrow{p_0}$.В таком случае интегрирование сводится к вычислению:
Соответственно имеем:
Если провести интегрирование по остальным зонам, то в результате убывания $\overrightarrow{p_{0\bot }}$их действие медленно убывает с ростом номера зоны (n), при $n\to \infty $ оно равно нулю. Что служит обоснование того, что метод зон Френеля применим к нашему случаю. Добавим $d\overrightarrow{E_1}$ к падающей волне, имеем:
где $dФ=\frac{2\pi k_0Np_0}{E_0}d\xi.$ Получаем, что присутствие слоя несет дополнительное отставание по фазе $dФ$. При конечной толщине слоя ($l$) $Ф$ равно:
Формула (8) - объяснение замедления фазовой скорости волны в среде.
Следует связать амплитуды $E_0\ и\ p_0$. В общем случае это сложная задача, постольку, поскольку дипольный момент атома $\overrightarrow{p}$ определён не средним макроскопическим полем $\overrightarrow{E}$, а микроскопическим полем, которое действует на атомы среды.
Объяснение процесса распространения волны при наличии теплового движения атомов
Ранее тепловое движение атомов мы не учитывали. Так почему при его наличии в веществе может распространяться регулярная волна и как может возникать правильное отражение от зеркальных поверхностей жидкостей и твердых тел?
Рассмотрим газ. В промежутках между столкновениями молекулы газа движутся равномерно и прямолинейно. Из-за существования эффекта Доплера атомы, которые имеют разные скорости, излучают свет с различными частотами. Однако изменение частоты нет, если речь идет о вторичных волнах, которые идут в направлении распространения света.
Пусть в газе распространяется плоская монохроматическая волна с частотой $\omega \ $системе отсчета $S$, где газ не движется. Рассмотрим атом, находящийся в движении. Свяжем с этим атомом систему отсчета $S'$. В системе отсчета $S'$ частота наблюдаемой волны будет ${{\mathbf \omega }}'.$ С такой же частотой в системе $S'$ будут возбуждены колебания атома и будут излучаться вторичные сферические волны. При обратном переходе в систему S частота ${{\mathbf \omega }}'$ излучаемой сферической волны изменится, и будет зависеть от направления излучения. Для излучения, которое идет в направлении первичной волны будет прежняя частота $\omega ,$ при этом не важно, в какую сторону и с какой скоростью двигался атом.
Так, в направлении распространения первичной волны все атомы излучают волны с одной и той же частотой $\omega .$ Именно с этим связана возможность регулярного распространения света в газе.
В твердых и жидких веществах атомы совершают колебания около положения равновесия и этим модулируют поле волны света. Как результат -- сохраняются вторичные волны с прежней частотой и появляются волны с новыми частотами. К излучению с сохранившимися частотами связана возможность регулярного распространения волн света, (их отражения и преломления) в данных веществах. Излучения с изменившимися частотами ведут к возникновению в рассеянном свете новых частот.
Задание: Чему равно отставание по фазе волны при прохождении через слой разреженного газа толщиной $l$, если показатель преломления газа равен $n$?
Решение:
Для неплотных газов (при $n-1\ll 1$) среднее макроскопическое поле $\overrightarrow{E}$ почти совпадает с микроскопическим полем, которое действует на атомы газа. В таком случае, можно записать:
\[{\overrightarrow{p}}_0=\beta \overrightarrow{E_0}\left(1.1\right),\]где $\beta $ -- поляризуемость атома, которая связана с диэлектрической проницаемостью соотношением:
\[\varepsilon =n^2=1+4\pi N\beta =1+4\pi N\frac{p_0}{E_0}\to \frac{p_0}{E_0}=\frac{n^2-1}{4\pi N}\left(1.2\right).\]При конечной толщине слоя ($l$) $Ф$ равно:
\[Ф=\frac{2\pi k_0Np_0}{E_0}l=\frac{n^2-1}{2}k_0l\left(1.3\right).\]Ответ: $Ф=\frac{n^2-1}{2}k_0l$.
Задание: Опишите ситуацию, которая сложится относительно волны, проходящей через слой вещества (рис.1), если точку наблюдения ($A$) разместить перед слоем.
Решение:
В ситуации, описанной в условии если средние расстояния между атомами меньше длины волны и атомы распределены в пространстве равномерно, то не появляется ни каких волн кроме прошедшей и отраженной.
В случае если расстояние между атомами больше длины волны, атомы в веществе распределены регулярно, то вторичные волны, которые излучают атомы, будут когерентными. Условия интерференционного усиления вторичных волн могут выполняться в направлениях падающего и отраженного света, а также некоторых других направлениях. Появляется дискретный ряд плоских волн, интерференционное рассеяние.
Если атомы вещества распределены в хаотичном порядке, то вторичные волны при боковом рассеянии некогерентны, значит, их интенсивности складываются.











