Явление дисперсии
Зависимость скорости распространения волны от ее частоты называют дисперсией. Дисперсия света - это результат взаимодействия электромагнитных волн (световых волн) с заряженными частицами, которые составляют вещество наряду с нейтральными частицами. Это явление сопровождается спектральным разложением немонохроматического света на синусоидальные составляющие. Происходит это потому, что разным частотам соответствуют различные показатели преломления. В вакууме все электромагнитные волны распространяются с одинаковой скоростью не зависимо от их частоты. Явление дисперсии возможно только в веществе. Значит ее объяснение связано со структурой вещества.
Существенная разница между ${\varepsilon }^2$ ($\varepsilon -диэлектрическая\ проницаемость\ $вещества) и $n$ (показатель преломления среды) имеется у веществ, которые имеют полярные молекулы, если $\varepsilon $ измеряется на частотах на много отличающихся от частоты волн света. Однако, измерения показателей преломления веществ в оптическом диапазоне, показали, что n одинаков у веществ с полярными и не полярными молекулами. Значит, можно сделать вывод о том, что ориентационная поляризуемость наблюдается в веществах с полярными молекулами в статическом поле или переменных полях малой частоты. В полях с высокой частотой молекулярный диполь не успевает поворачиваться, степень ориентации диполей при этом уменьшается, значит, уменьшается диэлектрическая проницаемость.
Закон дисперсии
Для объяснения зависимости показателя преломления вещества от частоты (то есть явления дисперсии) надо провести анализ механизма поляризации атома (молекулы) в электромагнитном поле волны света.
Электрическая составляющая электромагнитной волны действует на электрон. Воздействием магнитной составляющей обычно пренебрегают, так как скорость электрона мала в сравнении со скоростью света. Электрическая сила, с которой волна действует на оптический электрон и заставляет их совершать колебания, может быть записана как:
Вынужденные колебания электронного облака происходят по закону:
где $A=\frac{q_eE_0}{m({\omega }^2_0-{\omega }^2)}.$ - амплитуда, ${\omega }_0-круговая\ $частота собственных колебаний электрона, зависящая от природы атома, $\omega $ -- круговая частота колебаний волны. Изменение начальной фазы с нуля при $\omega {\omega }_0$ учитывают, вводя знак у амплитуды.
Наведенный полем дипольный момент молекулы совершает колебания по закону:
Используя выражение (3) получим значение поляризуемости молекулы ($\alpha $):
Диэлектрическую проницаемость вещества с полярными молекулами можно выразить как:
где $n_0$ -- концентрация молекул. Выражение (5) называют законом дисперсии.
Выражение (5) можно упростить, если учесть, что для газов электрическая восприимчивость ($\varkappa =n_0\alpha $)$\ \varkappa \ll 1,\ $следовательно, можно выполнить следующее:
Используя выражения (5) и (6), имеем:
При выводе закона дисперсии мы учитывали только воздействие внешнего поля световой волны на электронное облако молекулы и не учитывали межмолекулярного взаимодействия. Значит, закон в виде (6) выполняется только для газов. Но для качественного объяснения процесса дисперсии он применим для жидких и твердых тел. Кроме того выражение (6) имеет смысл только при условии, что частота волны существенно отлична от собственной частоты колебаний электрона.
График закона дисперсии в виде (7) показан на рис. 1. Более точная теория дисперсии, которая учитывает затухание и приводит к верной зависимости показателя преломления на всем диапазоне частот, дает график, который изображен сплошной линией рис.1.
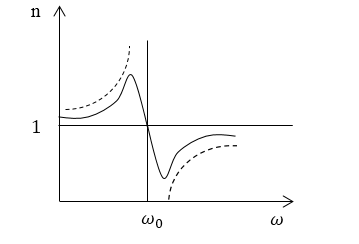
Рисунок 1.
Задание: Какова концентрация свободных электронов в ионосфере, если показатель преломления равен $n$ для радиоволн с частотой $\nu .$
Решение:
За основу решения задачи примем выражение:
\[n^2=1+\frac{n_0{q_e}^2}{m{\varepsilon }_0\left({\omega }^2_0-{\omega }^2\right)}\left(1.1\right),\]где $n_0$ - концентрация молекул.
Учтем, что для свободных электронов собственная частота равна нулю (${\omega }^2_0=0$). Частота $\nu $ связана с циклической частотой ($\omega $) как:
\[\omega =2\pi \nu \left(1.2\right).\]Соответственно формулу (1.1) преобразуем к виду:
\[n^2=1-\frac{n_0{q_e}^2}{m{\varepsilon }_0{\left(2\pi \nu \right)}^2}\left(1.3\right).\]Из выражения (1.3) получаем:
\[n_0=\frac{\left(1-n^2\right)m{\varepsilon }_0{\left(2\pi \nu \right)}^2}{{q_e}^2}.\]Ответ: $n_0=\frac{\left(1-n^2\right)m{\varepsilon }_0{\left(2\pi \nu \right)}^2}{{q_e}^2}.$
Задание: Во всех телах наблюдается не одна, а несколько полос поглощения. Для того чтобы это учесть в классической теории принимают, что вещество построено из частиц разного типа (электронов, ионов), которые ведут себя как затухающие гармонические осцилляторы, имеющие разные собственные частоты. В разреженных газах взаимодействием этих частиц можно пренебречь. Как можно записать выражение для коэффициента преломления подобного вещества исходя из классической теории дисперсии? Что можно сказать о поведении полученного выражения при этом?
Решение:
За основу решения задачи примем выражение для одного типа частиц вида:
\[n^2=1+\frac{n_0{q_e}^2}{m{\varepsilon }_0\left({\omega }^2_0-{\omega }^2\right)}\left(1.1\right).\]В таком случае искомая формула может быть представлена как:
\[n^2=1+\frac{n_0}{{\varepsilon }_0}\sum\limits_k{\frac{{q_e}^2}{m\left({\omega }^2_{0k}-{\omega }^2\right)}(1.2)},\]где ${\omega }_{k0}$ -- собственные частоты частиц, составляющих газ. Около каждой собственной частоты функция, представленная в (1.2) терпит разрыв. В том случае, если $\omega $ стремится к ${\omega }_{k0}$ слева, то функция $n(\omega )$ стремится к $+\infty $, если $\omega $ стремится к ${\omega }_{k0}$ справа, то $n\left(\omega \right)\to -\infty .$ Такое поведение функции объясняется тем, что если пренебрегать трением амплитуда вынужденных колебаний при резонансе становится бесконечной.











