Пусть поле $\overrightarrow{E}$ переставлено плоской волной:
где амплитуда поля переменна и равна:
Из формулы (2) следует, что в разных точках траектории электрон испытывает действие поля разной амплитуды. Что приводит к пространственной дисперсии. Этим фактом можно пренебречь, если считать, что амплитуда колебаний электрона мала в сравнении с длиной волны. Уравнение движение электрона при этом можно записать как:
где ${\omega }^2_0=\frac{k}{m}$, $2\gamma =\frac{g}{m}.$ Для теории дисперсии значение имеет только частное решение уравнения (3), которое представляет вынужденные колебания осциллятора:
Амплитуда $\overrightarrow{r_0}$ находится подстановкой выражения (4) в формулу (3), получаем:
Атом в электрическом поле имеет дипольный момент равный:
где $\beta -\ $поляризуемость атома, она определяется как:
В том случае, если $N$ -- концентрация атомов, то вектор поляризации среды равен:
Вектор индукции:
где $\varepsilon $ получается равной:
Очевидно, что материальное уравнение (9) имеет вид такой же как в теории Максвелла. Только диэлектрическая проницаемость зависит от частоты. Следовательно, имеют силу все полученные в магнетизме результаты при замене постоянной $\varepsilon $ на функцию $\varepsilon \left(\omega \right).$ При этом функция $\varepsilon \left(\omega \right)$ является комплексной. Представим показатель преломления в комплексном виде:
где $n$- вещественный показатель преломления, $\varkappa $ -- показатель затухания среды. Возведем выражение (11) в квадрат, (10), имеем:
Далеко от$\ {\omega }_0$, где $2\omega \gamma \ll \left|{\omega }^2_0-{\omega }^2\right|$ мнимой частью выражения (10) можно пренебречь, при этом коэффициент преломления ($n$) можно выразить:
До сих пор мы считали, что у каждого вещества есть одна характерная для него циклическая частота ${\omega }_0$ свободных колебаний электронов. В реальности, при распространении волны света в среде определяется ряд характерных для каждого вещества линий поглощения. Значит, любое вещество характеризуют набором разных частот ${\omega }_{0k}.$ При воздействии поля волны света все данные осцилляторы совершают вынужденные колебания, внося вклад в поляризацию вещества. Чтобы это учесть в классической теории, принимают то, что среда состоит из частиц разного типа: электронов и ионов. Данные частицы ведут себя как затухающие частицы, совершающие затухающие гармонические колебания с разными собственными частотами. В газах взаимодействием частиц пренебрегают, следовательно, в выражение для диэлектрической проницаемости приобретет вид:
где индекс указывает на принадлежность параметра осциллятору с номером $k$.
Приближенная формула для вычисления показателя преломления может быть записана как:
Каждой собственной частоте соответствует своя линия поглощения, около которой показатель преломления изменяется аномально. Общий ход функции $n\left(\omega \right)$ на рис.1.
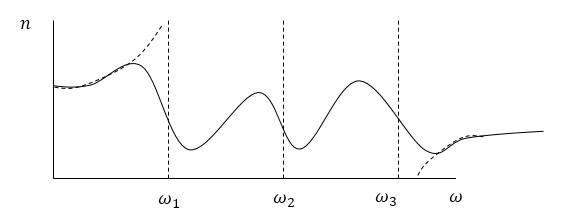
Рисунок 1.
Рассмотрите предельные случаи, ответьте на вопрос как ведет себя показатель преломления вещества в случаях: 1) если частота волны существенно отлична от собственной частоты колебания заряженной частицы; 2) частота стремится к собственной частоте?
Решение:
Рассмотрим выражение для $n^2(\omega )$:
\[n^2=1+\frac{N_k}{{\varepsilon }_0}\sum\limits_k{\frac{\frac{{q_{ek}}^2}{m_k}}{{\omega }^2_{0k}-{\omega }^2}}\left(1.1\right).\]При частотах существенно отличающихся от всех собственных частот (${\omega }_{ok}$) сумма $\frac{N_k}{{\varepsilon }_0}\sum\limits_k{\frac{\frac{{q_{ek}}^2}{m_k}}{{\omega }^2_{0k}-{\omega }^2}}\ll 1$, следовательно, $n^2\approx 1.$
Около каждой из собственных частот функция $n^2(\omega )$ при приближении $\omega $ к ${\omega }_{0k}\ $слева она стремится к $+\infty .$ При стремлении частоты $\omega $ справа к ${\omega }_{0k}$ функция $n^2\left(\omega \right)\to -\infty .$ Данное поведение функции $n^2(\omega )$ объясняется тем, что мы пренебрегли трением излучения, а пренебрежение трением ведет в вынужденных колебаниях к тому, что при резонансе амплитуда становится бесконечной. Если терние учтено, то функция $n^2(\omega )$ приобретает вид, указанный на рис.1
Что из себя представляет кривая зависимости $n(\lambda )$ в области резонансных частот. Укажите участки кривой, соответствующие нормальной и аномальной дисперсии.
Решение:
Переходя от $n^2$ к $n$ и от частоты к длине волны, получим кривую в области резонансных частот, которая изображена на рис.2. Пунктир показывает ход коэффициента поглощения света веществом. Участок 3-4 аналогичен кривой, рис.1. Участки 1-2 и 3-4 соответствуют нормальной дисперсии ($\frac{dn}{d{\lambda }_0}0$). В области нормальной дисперсии $\frac{dv}{d\lambda } >0,$ групповая скорость получается меньше скорости света в вакууме. В области аномальной дисперсии понятие групповой скорости теряет смысл из-за слишком большого поглощения.











