Интерференция поляризованных лучей исследовалась в опытах Френеля и Араго. Поляризованные лучи от некогерентных источников света не будут подвергаться интерференции. Но интерференционная картина линейно поляризованных лучей зависит от угла между плоскостями, в которых происходят световые колебания. Интерференционные полосы имеют максимальную контрастность тогда, когда плоскости колебаний параллельны. Интерференционную картину невозможно получить, если поляризация волн во взаимно перпендикулярных плоскостях. Что и было получено эмпирически Араго и Френелем. Именно из этих опытов Френель сделал вывод о поперечности колебаний в волне света.
Пусть пучки света от источника света $S$ распространяются через поляроид (П) рис.1. Вторичные когерентные источники $S_1\ и\ S_2$ получают одним из способов, которые используют для реализации двухлучевой интерференции. При этом исходящие пучки света от $S_1\ и\ S_2$ поляризованы в параллельных плоскостях. На пути распространения одного из пучков ставится полуволновая кристаллическая пластина ($K$). На ходу другого пучка помещают стеклянную пластинку ($P$) для того, чтобы компенсировать появившуюся разность хода. Стеклянная пластина не изменяет направления колебаний линейно поляризованной волны. Пластина ($K$) действует аналогично, только если ее оптическая ось параллельна или перпендикулярна плоскости колебаний электрического вектора волны. Тогда из пластинок $K$ и $P$ выходят одинаково поляризованные когерентные лучи. Направления колебаний изображены векторами $\overrightarrow{E_1\ }и\ \overrightarrow{E_2\ }$, которые совпадают (рис.1).
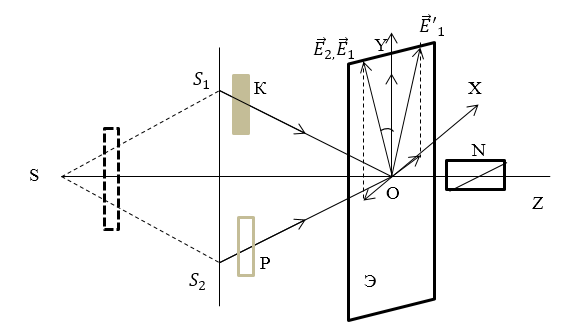
Рисунок 1.
При повороте пластинки $K$ вокруг ее нормали на угол $\alpha $ получим поворот вектора $\overrightarrow{E_1}$ на угол $2\alpha $, и займет положение $\overrightarrow{E_1}'$. Так, можно изучать интерференцию при разных углах ($\alpha $) между плоскостями колебаний волн.
Картину интерференции получают на экране (Э рис.1) или можно наблюдать без экрана в зрительную трубу. В плоскости экрана расположим координатную плоскость $XY$. Оптическая ось пластинки $K$ будет направлена по оси $Y$, нормаль к экрану (в сторону распространения света) -- ось $Z$. Так, при повороте пластинки будет вращаться и ось $Y$.
В результате суперпозиции линейно поляризованных монохроматических волн всюду (и на экране) появится эллиптическая поляризация света. Если оставить постоянным угол между плоскостями колебаний, то форма и ориентация эллипса колебаний будет меняться при изменении разности хода между интерферирующими лучами. При некоторых значениях разности хода эллиптические колебания могут вырождаться в линейные. Поверхности (на экране линии) одинаковой разности хода -- это поверхности (линии) одинаковых и одинаково ориентированных эллипсов колебаний.
Интерференция при прохождении поляризованного света через кристалл
Допустим, что на плоскопараллельную пластинку падает волна под углом $\varphi $ (рис.2).
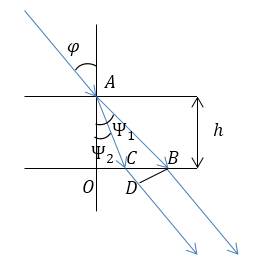
Рисунок 2.
В кристалле волна делится на две, распространяющиеся в разных направлениях и имеющие разные скорости. Обозначим волновые нормали как $AB$ и $AC$ данных волн. При этом $\Psi_1$ и $\Psi_2$ будут соответствующие им углы преломления. Вне кристалла направления волновых нормалей одинаково. Из кристалла выходят два параллельных луча. Разность хода ($\triangle $) этих лучей будет равна:
где $n_2$ и $n_2$ -- показатели преломления рассматриваемых волн, $h$ -- толщина пластинки. Разность хода лучей вызвана:
- разными показателями преломления волн,
- разными углами преломления.
Часто разницей в углах преломления пренебрегают и используют выражение:
где $\Psi$ -- угол имеет любое значение между углами $\Psi_2\ и\ \Psi_1$. Возникающая при такой ситуации разность фаз различна для разных длин волн, в результате интерференционная картина окрашивается. Для плоскопараллельных пластинок наблюдают полосы равного наклона, для тонких клиньев -- полосы равной толщины.
Систему поляризатор -- пластинка -- анализатор применяют для исследования картины интерференции в параллельных лучах. Формула:
(где $\delta $ -- разность фаз) дает возможность для любой фазовой пластинки найти интенсивность на выходе при скрещенных поляризаторе и анализаторе и заданной ориентации оптической пластинки (угол $\varphi $).
Интерференция поляризованных лучей предоставляет удобный метод нахождения и изучения оптической анизотропии. Для этого обычно применяют установки в параллельных лучах со скрещенными николями.
Более сложные явления возникают при интерференции сходящихся поляризованных лучей. Наблюдаются так называемые коноскопичекие картины. Возникающие за анализатором линии постоянной разности фаз называют в таком случае изохроматами.
Демонстрации по интерференции поляризованных лучей в большинстве случаев проводят с тонкими пластинками. Почему? Почему, даже используя пластинки из исландского шпата небольшой толщины тяжело получить интерференционную картину в белом свете?
Решение:
-
В соответствии с выражение для разности хода лучей ($\triangle $), поляризованного света выходящих из кристалла:
\[\triangle =hcos\left(n_2-n_1\right)\left(1.1\right)\]зависит от толщины пластины. При очень большой разности хода интерференция в белом свете получаться не будет, поэтому используют тонкие пластины.
-
У исландского шпата очень большая разность обыкновенного и необыкновенного показателей преломления, следовательно, даже для пластинок малой толщины получаются большие разности хода в соответствии с формулой (1.1)$.$
А при большой разности хода интерференция в белом свете невозможна.
Две пластинки большой толщины одноосного кристалла ориентированы одинаково. Они мало отличаются по толщине и в скрещенных николях дают (отдельно друг от друга) белый свет. Почему в тех же условиях модно получить окрашивание, если осуществить поворот одной пластины относительно другой на угол $\frac{\pi }{2}?$
Решение:
В случае одинаковой ориентации пластинок, разность хода, которую они вносят, мала, то есть соответствует порядку интерференции. Если осуществить поворот, который обозначен в условиях задачи, то создаваемая им разность хода станет такой, как вносит пластинка с толщиной равной разности толщин заданных пластинок. Если разность толщин мала, разность хода может стать такой небольшой, что появится возможность интерференции в белом свете.












