Дифракция на акустических волнах

Качественное описание дифракции света на акустических волнах

Дифракцию световой волны на акустических волнах изучает задел физики, который называют акустооптикой. Это область физики, являющаяся пограничной между оптикой и техникой предметом изучения которой являются явления связанные со взаимодействием электромагнитных и звуковых волн. На основании полученных знаний создаются технологии применения изученных явлений в технике. Такие явления используют в оптоэлектронике, технике лазеров, в области обработки информации. Технические устройства и приборы, разработанные в рамках акустооптики, дают возможность управления амплитудой, частотой, составом спектра световой волны.

Различают два вида дифракции, которые отличны дифракционными спектрами -- это Рамана - Ната и Брэгга. Первый вид дифракции наблюдают на низких звуковых частотах и небольшой глубине акустического поля. При нормальном падении (параллельно волновому фронту звуковой волны), дифракционный спектр Рамана - Ната -- симметричный (относительно прошедшего пучка), равноотстоящую друг от друга систему максимумов дифракции. При наклонном падении света интенсивность максимумов уменьшается, угловые направления неизменны. Дифракцией Брэгга называют дифракцию, когда максимумами минус первого и высших порядков можно пренебречь. При этом интенсивность первого максимума наибольшая. При чем интенсивность первого максимума наибольшая, если световая волна падает под углом к волновому фронту звука под углом Брэгга ${\theta }_B$, который удовлетворяет условию: $sin{\theta }_B=\frac{\lambda }{2\Lambda }.$

Дифракция Брэгга рассматривается на высоких частотах, при большой длине взаимодействия света с акустической волной.

Вид дифракции определяют, используя параметр $Q$, равный:

где $L$ - длина звукового столба. Приближенно считают, что при $Q\ll 1$ имеет место дифракция Рамана -- Ната, при $Q\gg 1$ -- дифракция Брэгга.

Распространяясь в веществе, звуковая волна вызывает механическую деформацию среды, следовательно, пространственную модуляцию ее оптических свойств (точнее акустическая волна создает периодическое распределение показателя преломления вещества). Частота изменения оптических свойств среды равна частоте волны звука. Частота звуковых колебаний существенно меньше, чем частота электромагнитных колебаний в волне света. То есть оптические свойства среды изменяются во времени гораздо медленнее, чем распространяется луч света сквозь пучок звука. При прохождении света через звуковой пучок возможны два явления (это зависит от отношения $\frac{d}{{\lambda }_{zv}},\ где\ d$ -- диметра пучка света, ${\lambda }_{zv}-длина\ волны\ звука$): рефракция и дифракция света на ультразвуке.

В 1921 г. Бриллюэн предсказал, если освещать жидкость, в которой присутствуют упругие волны малой длины, светом, то появляется дифракция, подобная дифракции на решетке. Практически через 10 лет Дебай и Сирс и отдельно от них Люка и Бикар эмпирически убедились в дифракции света на ультразвуковых волнах.

Допустим, что жидкость находится между двумя бесконечными плоскостями: $y=0$, $y=d$ и пусть плоская упругая волна длиной $\Lambda $ распространяется по оси $X$. Такое движение создает периодическую слоистость в жидкости по оси $X$, при этом расстояние между последовательными плоскостями равно $\Lambda $.

Монохромная волна света с угловой частотой $\omega $ и длиной волны в жидкости $\widetilde{\lambda },$ падает в выше описанною жидкость. Нормаль к волновой поверхности расположена в плоскости $XY$ и составляет угол $\widetilde{\theta }$ с осью $Y$ (рис.1). Через угол $\widetilde{\varphi }$ обозначим угол, который образует луч света после дифракции с осью $Y$. Скорость звуковых волн много меньше скорости света, поэтому будем считать, что слоистая структура вещества неподвижна. Значит, можно сказать, что направление $\widetilde{\varphi },$ в котором имеется заметная интенсивность, определяют из условия: оптическая разность хода лучей соседних плоскостей равна величине кратной длине волны $\widetilde{\lambda }$:

где $AB$ и $CD$ -- части фронтов волны, которые связаны с преломленными и дифрагированными лучами. Использовав закон преломления, получаем:

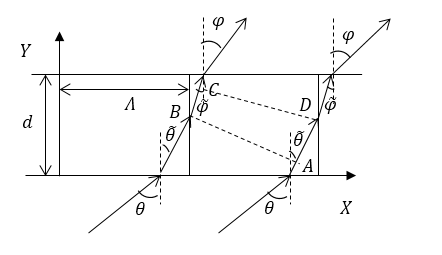
Рисунок 1.

Угловое расстояние из (3) получаем:

Пусть $N(\overrightarrow{r},t)$ -- концентрация атомов (молекул) в среде. Для плоской упругой волны, распространяющейся в однородной изотропной среде по оси $X$, запишем:

где $N_0$ -- средняя концентрация молекул в веществе, $N_0\triangle $ - амплитуда звуковой волны, $K-$ -- волновой вектор упругой волны, $\Omega =Kv$ -- угловая частота звукового излучения. В нашем случае диэлектрическая проницаемость среды будет зависеть от пространственных координат и времени:

где ${\varepsilon }_1=\gamma \triangle ,$ $\gamma =\frac{1}{3}\left({\varepsilon }_0-1\right)\left({\varepsilon }_0+2\right)-Для\ большого\ числа\ жидкостей\ \gamma \ \approx 1.$ Кроме того:

где углы $\theta $, $\varphi ,\dots $ изменяются по часовой стрелке от положительного направления оси $Y$ по направлению распространения света, $0\le \theta \le \frac{\pi }{2}.$

Уравнения Максвелла и дифракция на акустических волнах

Дифракцию световой волны на звуке можно описать, учитывая в уравнениях состояния среды, перекрестные члены соответствующие и электромагнитному полю и упругим деформациям. Значит, электромагнитная и звуковая волны будут удовлетворять уравнениям Максвелла и уравнению движения (механика). Так, соответствующий перекрестный член запишем как:

где ${\varepsilon }^0_{ij}$ - тензор диэлектрической проницаемости, $f_{ijki}$ - тензор электрострикции, $e_{ijk}$ -- пьезомодули. Слагаемое $\delta {\varepsilon }_{ij}=f_{ijki}u_{ki}$ -- рассматривают как изменение диэлектрической проницаемости, которое вызвано волной звука. Иногда, $\delta {\varepsilon }_{ij}$ записывают через фотоупругие коэффициенты ($p_{klmn}$):

Если считать, что пьезоэффекта нет, то из уравнений Максвелла и выражения (8) следует, что уравнение для электрического поля можно записать как:

Пусть на поверхность периодической слоистой жидкости (рис.1) падает линейно поляризованная монохроматическая плоская волна (электрический вектор направлен вдоль оси $Z$). У равнение для $E_z$ примет вид:

Для решения уравнения (11) полагают, что:

где сумма берется по всем целым $l$. Для $V_l(y)$ имеются рекурентные соотношения:

где ${V^{''}}_l\left(y\right)=\frac{d^2V_l(y)}{dy^2}$. Граничные условия для уравнений:

Рисунок 2.

Раман и Натом решили уравнения (13). Их решение объяснило возникновение спектров многих порядков при рассматриваемом виде дифракции. Эти учены положили:

Учли, что $\frac{\Omega }{\omega }\approx {10}^{-5}$, $\tilde{k}=nk,\ ksin\theta =\tilde{k}sin\widetilde{\theta }.$ При $\frac{\lambda }{d}\ll 1$ получили интенсивность в спектре порядка $l\ $вида: $B^2J^2_l(\frac{1}{2}{\varepsilon }_1{{\varepsilon }_0}^{-1}\tilde{k}dsec\widetilde{\theta })$, где $J_l$ -- функция Бесселя.

Отметим, что допущение Рамана и Ната основывается на малости величин: $\frac{l^2}{\delta }\ и\ \frac{l\xi }{\delta }$ для всех $l$. Следовательно, если $\delta \ $велико относительно 1, то принятое приближение хорошо описывает интенсивности низших (но не высших) порядков. Другая интерпретация дифракции на акустических волнах дана Вагнером.

Особенности дифракции света на поверхностных акустических волнах заключаются в том, что связь упругого и электромагнитного полей реализуется через механизм фотоупругости и за счет искажений поверхности, которые сопровождают распространение данных волн.