Результат дифракции монохроматического излучения на препятствии зависит не от размеров препятствия, а от количества зон Френеля ($m$), которые перекрывает это препятствие.
Так при $m\gg 1$ (имеется в виду числа порядка сотен и тысяч открытых зон) картина дифракции не существенна и распространение света описывается законами геометрической оптики. Промежуточным состоянием является ситуация, когда открыты единицы или десятки зон. Такое положение вещей соответствует дифракции Френеля, что означает возможность наблюдения сложного распределения интенсивности, когда можно наблюдать чередование максимумов и минимумов интенсивности света.
При $m
Условной границей между двумя видами дифракции называют дистанцию Рэлея ($R$) или дифракционную длину (что одно и то же). И так, дифракционная длина определяет границу (весьма условную) между ближней и дальней зонами дифракции. Величина $R$ соответствует расстоянию, при котором круглое отверстие, имеющее диаметр $d$, при освещении его плоско монохроматической волной ($\lambda $) открывает для центральной точки наблюдения одну первую зону. Математически это записывается так:
Картина фраунгоферовой дифракции имеет эквивалентный характер. Она линейно увеличивается в поперечном направлении при увеличении расстояния от экрана с отверстием. Угловой размер центрального дифракционного максимума в дальней зоне определен отношением длины волны света к диаметру отверстия. Область, в которой работают законы геометрической оптики для отверстия порядка микрон, будет иметь размер порядка миллиметра. Для отверстий около сантиметра область «геометрической оптики» достигает сотни метров.
Дифракционная длина связана с количеством зон Френеля (m), так нам известно, что:
где $l$ -- расстояние от препятствия до экрана. В таком случае для дифракционной длины можно записать:
Из выражения (3) следуют условия для разделения зон дифракции на ближнюю и дальнюю:

Рисунок 1.
Задание: Какова дистанция Рэлея для монохроматического света с длиной волны $\lambda =0,5\ мкм$ для отверстий диаметром: 1) $d_1=0,1\ мм;\ 2)\ d_2=1\ мкм$? Чему равно количество открытых зон Френеля для отверстия, диаметр которого равен ${10}^{-2}м$, если экран находится на расстоянии $1 м$, какую величину при этом составит дифракционная длина?
Решение:
В качестве оценочной формулы используем выражение:
\[R=\frac{d^2}{\lambda }\left(1.1\right).\]Переведем единицы необходимых для расчета величин в систему СИ:
\[\lambda =0,5\ мкм=5\cdot {10}^{-7}м,\ d_1=1\ мм={10}^{-3}м;;\ 2)\ d_2=1\ мкм={10}^{-6}м.\]Проведем вычисления:
\[R_1=\frac{{\left({10}^{-4}\right)}^2}{5\cdot {10}^{-7}}=2\left(м\right).\] \[R_2=\frac{{\left({10}^{-6}\right)}^2}{5\cdot {10}^{-7}}=2\cdot {10}^{-7}\left(м\right).\]- Количество открытых зон Френеля найдем по формуле:
Проведем вычисления:
\[m=\frac{{\left({10}^{-2}\right)}^2}{1\cdot 5\cdot {10}^{-7}}=200.\]При этом дифракционная длина может быть вычислена по формуле:
\[R=m\cdot l\ \left(1.3\right).\]Расчет дает:
\[R=200\cdot 1=200\ \left(м\right).\]Ответ: 1) $R_1=2$м; $R_2=2\cdot {10}^{-7}м.$ 2) $m=200$, $R=200м$.
Задание: Объясните, почему дистанция Рэлея является важным параметром при рассмотрении явления дифракции?
Решение:
Не смотря на то, что граница между дифракцией Френеля и дифракцией Фраунгофера весьма условна, для применения разных подходов к расчету полей (разных приближений) стоит использовать такой параметр как дифракционная длина, для понимания какую зону дифракции (ближнюю или дальнюю) предстоит изучать. Так для этих зон можно выделить следующие различия:
К особенностям ближней зоны дифракции относят:
-
Для оси пучка света считается, что интенсивность постоянна и равна интенсивности исходящей от источника интенсивности.
-
Структура пучка света остается постоянной и задается формой отверстия. В пределах отверстия может располагаться множество зон Френеля.
Особенностями дальней зоны дифракции являются:
-
Интенсивность исходной световой волны много больше, чем интенсивность света на оси пучка. Интенсивность света на оси пучка уменьшается в зависимости от расстояния до источника (она обратно пропорциональна квадрату расстояния).
-
Световой пучок, по мере распространения от источника, расширяется. В границах отверстия размещается только одна малая центральная часть зоны Френеля номер один.
Соответственно, для дифракции Френеля применяют соответствующее приближение для расстояний:
\[r=l+\frac{{\left(x-x'\right)}^2+{\left(y-y'\right)}^2}{2l}\left(2.1\right).\]При рассмотрении дифракции Фраунгофера, которая в практических приложениях встречается чаще, используют приближение Фраунгофера вида:
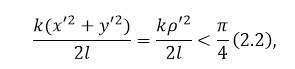
Рисунок 2.
где ${ρ}'^2={x'}^2+{y'}^2$ – максимальное расстояние от центра отверстия до его края, на котором идет дифракция.
Использование соответствующих приближений упрощает решение задач дифракции.











