Область дифракции Френеля
Явления дифракции классифицируют в зависимости от расстояний источника и точки наблюдения (экрана) до препятствий, которые находятся на пути световой волны.
Область дифракции, которая расположена недалеко от объекта, на котором происходит дифракция, называется ближней зоной дифракции или областью дифракции Френеля. Эта зона доходит до расстояний, с которых можно рассматривать дифракцию как фраунгоферову. В дифракционных задачах, использующих подходы Френеля нельзя пренебрегать кривизной поверхности волны, которая падает на препятствие (отверстие) и волны после дифракции. При дифракции Френеля на экране получают «дифракционное изображение» препятствия. Аналитический расчет дифракционных задач Френеля составляет существенные трудности.
В большинстве случаев на практике для описания дифракции Френеля используют приближение Френеля и получают выражение:
где $dS'=dx'dy'$- элемент на поверхности источника света, $(x,y)$ -- координаты какой -- то точки (A) в плоскости дифракционной картины, $(x',y')$- координаты точки ($A'$) интегрирования в плоскости источников, $\Psi \left(x',y'\right)=\frac{Ce^{ikr_{12}}}{r_{12}}$ -- амплитуда источников, $l$- расстояние между плоскостью дифракционной картины и плоскостью источников. Данную формулу часто используют, отбрасывая множитель $\frac{k}{2\pi i}\frac{e^{ikl}}{l}$, так как он не влияет на относительное распределение интенсивностей в дифракционной картине.
В простейших случаях для того, чтобы установить вид картины дифракции используют метод кольцевых зон Френеля, спираль Корню.
К особенностям ближней зоны дифракции относят:
-
Для оси пучка света считается, что интенсивность постоянна и равна интенсивности исходящей от источника интенсивности.
-
Структура пучка света остается постоянной и задается формой отверстия. В пределах отверстия может располагаться множество зон Френеля.
Дальня зона дифракции (дифракция Фраунгофера)
В том случае, если расстояния от источника и точки наблюдения до препятствия велики (бесконечны), то дифракция называется дифракцией в параллельных лучах или дифракцией Фраунгофера. Область дифракции Фраунгофера простирается от бесконечности до некоторого минимального расстояния. На практике реализация дифракции Фраунгофера выполняется, если точечный источник световых волн размещают в фокусе собирающей линзы. Получившийся при этом параллельный пучок света совершает дифракцию на препятствии. Дифракционную картину наблюдают в фокальной плоскости линзы, которая размещается на пути света совершившего дифракцию или используют зрительную трубу, которую устанавливают на бесконечность. Картина дифракции является дифракционным изображением источника света. Этот вид дифракции рассчитывают, используя аналитические методы.
Распределение интенсивности в дифракционной картине определяется квадратом модуля $Ф(x,y).$ Для дифракции Фраунгофера имеем:
Формула (2) служит для вычисления относительных величин интенсивностей в картине дифракции.
Особенностями дальней зоны дифракции являются:
-
Интенсивность исходной световой волны много больше, чем интенсивность света на оси пучка. Интенсивность света на оси пучка уменьшается в зависимости от расстояния до источника (она обратно пропорциональна квадрату расстояния).
-
Световой пучок, по мере распространения от источника, расширяется. В границах отверстия размещается только одна малая центральная часть зоны Френеля номер один.
Рассмотрим круглое отверстие и точечный источник света, который расположен на его оси (рис. 1).
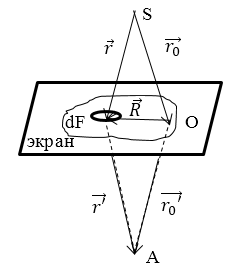
Рисунок 1.
Допустим, что точка наблюдения находится также на оси. В том случае, если в отверстии укладывается часть первой зоны Френеля, то такая дифракция является фраунгоферовой. В данном случае все колебания в плоскости отверстия происходят и попадают в точку наблюдения в одинаковых фазах. При смещении точки наблюдения от оси, возникают разности фаз между вторичными волнами, которые попадают в точку наблюдения от разных точек отверстия, что вызывает появление дифракционных колец. Если отверстие заменяется непрозрачным экраном, то данный случай так же отнесем к дифракции Фраунгофера. В том случае, если в отверстии или экране (для точки наблюдения на оси системы) укладывается существенная часть первой зоны или несколько зон Френеля, то дифракцию называют френелевой.
Вообще говоря, между фраунгоферовой и френелевой дифракциями нет принципиального различия и резкой границы.
Характер дифракции можно определять следующими критериями:

Рисунок 2.
где $l$ -- расстояние от препятствия до экрана, $b$ -- ширина щели (диаметр/радиус). Параметр $p$ для точки находящейся напротив середины щели можно связать с числом зон Френеля, открываемых щелью ($m$):
Задание: Объясните, как распределяется интенсивность в ближней зоне дифракции, как она распределяется в дальней зоне, если рассматривать дифракцию от щели?
Решение:
В ближней зоне дифракции, когда щель открывает большое количество зон Френеля ($m\gg 1$) на экране получают равномерное освещение изображения щели. Только у границ геометрической тени имеются почти незаметные узкие полосы максимумов и минимумов. При малых расстояниях от экрана до щели изображение соответствует законам геометрической оптики. Если расстояние увеличивать, то получим сначала дифракционную картину Френеля, которая перейдет в картину дифракции Фраунгофера. Такую последовательность изменений можно получать, если уменьшать ширину щели при неизменном расстоянии. В случае $m\sim 1$, на экране получается изображение щели, по краям у которой, отчетливо видны светлые и темные полосы.
Если щель открывает малую часть центральной зоны Френеля ($m\ll 1$), то наблюдается дифракция в дальней зоне. Распределение интенсивности можно изобразить кривой (рис.3).
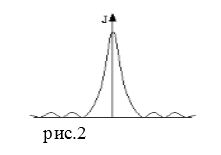
Рисунок 3.
Задание: В какой зоне рассматривается дифракция, если параллельный пучок света имеющий длину волны $\lambda =0,6 мкм$ падает перпендикулярно на круглое отверстие диаметр которого $d=1 мм$. При этом образуется картина дифракции на экране, который расположен на расстоянии $l=50 см$.
Решение:
Для ответа на вопрос задачи следует вычислить параметр
\[p=\frac{d^2}{l\lambda }(2.1)\]Переведем данные в систему СИ:
\[\lambda =0,6\ мкм=0,6\cdot {10}^{-6}м,\ \ d=1мм={10}^{-3}м,\ \ \ l=50\ см=0,5м.\]Проведем расчет, используя формулу (2.1):
\[p=\frac{{\left({10}^{-3}\right)}^2}{0,5\cdot 0,6\cdot {10}^{-6}}\approx 3.\]Согласно критерию:

Рисунок 4.
В данном случае имеют дело с дифракцией Френеля.
Ответ: Ближняя зона дифракции.











