Из закона о равномерном распределении энергии по степеням свободы молекулы газы мы запомнили, что в идеальном газе при умеренных температурах на каждую степень свободы приходится энергия равная $\left\langle \varepsilon \right\rangle =\frac{i}{2}kT.$ Логично предположить, что все суммарная энергия молекул газа может быть рассчитана как:
где N -- число молекул газа, i -- число степеней свободы газа, k -- постоянная Больцмана, T -- термодинамическая температура. Если учесть, что
$N_{A\ }=6,02\cdot {10}^{23}моль^{-1}$ --постоянная Авогадро, $\nu $- число молей газа, то выражение для внутренней энергии (1) можно записать в виде:
где R= 8,31 $\frac{Дж}{мольК}$ -- универсальная газовая постоянная.
Внутренняя энергия системы
Во всех уравнениях U - это внутренняя энергия идеального газа. Внутренняя энергия системы важная функция состояния, ее изменение не зависит от способа перехода системы из состояния 1 в состояние 2.
Для газа, на который не действуют внешние силы, находящийся в состоянии макроскопического равновесия, внутренняя энергия представляет собой полную энергию системы. Внутренняя энергия включает в себя энергию теплового (хаотического) движения частиц и энергию их взаимодействия.
Внутренняя энергия газа является аддитивной, то есть полная внутренняя энергия системы есть сумма внутренних энергий ее макро частей. При невысоких температурах часто внутреннюю энергию идеального газа принимают равной суммарной кинетической энергии его молекул. Внутренняя энергия идеального газа зависит от термодинамической температуры T.
Что такое теплоемкость
Рассмотрим теперь что такое теплоемкость. Количество теплоты, переданное телу с целью нагреть его на 1К -- теплоемкость тела (системы). Обычно обозначается |C":
Теплоемкость единицы массы тела:
удельная теплоемкость.
Теплоемкость единицы молярной массы тела:
молярная теплоемкость.
Мы видим, что теплоемкость определена через понятие -- теплота. А нам известно, что количество тепла подведенного к системе зависит от процесса. Соответственно получается, что и теплоемкость зависит от процесса. Поэтому формулу определения теплоемкости (4) следует уточнить и записать в виде:
теплоёмкости (газа) в постоянном объеме и при постоянном давлении.
Найдем связь между внутренней энергией идеального газа и его теплоемкостью. Для этого запишем первое начало термодинамики:
Разделим обе части выражения (9) на dT, получим:
Очевидно, что в уравнении (10) в левой части стоит теплоемкость для изохорного процесса, а в левую часть подставим выражение для dU, полученное из уравнения (2):
В таком случае молярная теплоемкость при изохорном процессе будет иметь вид:
\[c_{\mu V}=\frac{i}{2}R\ \left(12\right).\]Из выражения (12) видно, что молярная теплоемкость идеального газа при постоянном объеме зависит только от числа степеней свободы молекулы газа и является величиной постоянной.
Рассмотрим изобарный процесс (p=const). Используем снова первое начало термодинамики, запишем его разделив правую и левую части на dT и отметим, что имеем дело с изобарным процессом:
\[{\left(\frac{\delta Q}{dT}\right)}_p=\frac{dU}{dT}+\frac{pdV}{dT}=\frac{i}{2}\nu R+\frac{pdV}{dT}\ \left(13\right).\]В правой части уравнения (13) мы получили теплоемкость газа при изохорном процессе. Для того, чтобы преобразовать второе слагаемое в правой части, используем уравнение Менделеева -- Клайперона:
\[pV=\nu RT\ \left(14\right).\]Если мы имеем дела с изобарным процессом, продифференцируем (14), получим:
\[pdV=\nu RdT\ \left(15\right).\]Подставим (15) в (13), получим:
\[С_p=\frac{i}{2}\nu R+\frac{\nu RdT}{dT}=\frac{i}{2}\nu R+\nu R\left(16\right).\]В таком случае молярная теплоемкость идеального газа при постоянном давлении получит выражение:
\[c_{\mu p}=\frac{i}{2}R+R=c_{\mu V}+R\left(17\right).\]Соотношение (17) между теплоемкостями идеального газа также называют соотношением Майера. Из уравнения (17) видно, что теплоемкость изобарного процесса больше, чем теплоемкость изохорного. Это и понятно. При изохорном процессе теплота идет только на изменение внутренней энергии газа, а при изобарном процессе теплота идет еще и на совершение газом работы.
Задание: Получите уравнение, связывающее показатель адиабаты ($\gamma$), используемый в одноименном процессе, с молярными теплоемкостями $c_{\mu V}\ $и $c_{\mu p}$.
Решение:
Итак, рассмотри адиабатный процесс. Он характеризуется тем, что все процессы в системе происходят без подвода к ней тепла. То есть $\delta Q=0.$ Соответственно, первое начало термодинамики имеет вид:
\[0=dU+pdV\ \left(1.1\right),\]где $dU=c_{мV}\nu dT$.
Из уравнения Менделеева -- Клайперона выразим давление:
\[p=\frac{\nu RT}{V}\left(1.2\right),\]подставим $\left(1.2\right)\ $в (1.1) и проведем разделение переменных:
\[c_{\mu V}\nu dT=-\frac{\nu RT}{V}dV\to c_{\mu V}dT=-\frac{RT}{V}dV\ \to \frac{dT}{T}=-R\frac{dV}{c_{\mu V}V}\left(1.3\right).\]Интегрируем (1.3), получим:
\[ln\left(T\right)=-\frac{R}{c_{\mu V}}{ln \left(V\right)+A\ }\left(1.4\right),\ A=const\]Потенцируем выражение (1.4), имеем:
\[T=AV^{\frac{c_{\mu V}-c_{\mu p}}{c_{\mu V}}}\to TV^{\frac{{c_{\mu p}-c}_{\mu V}}{c_{\mu V}}}=const\ (1.5),\]Уравнение адиабатного процесса в параметрах Т(V) имеет вид:
\[TV^{\gamma -1}=const\ \left(1.6\right).\]Следовательно, $\gamma$=$\frac{c_{\mu p}}{c_{\mu V}}$, где $\gamma$ -- показатель адиабаты.
Ответ: $\gamma$=$\frac{c_{\mu p}}{c_{\mu V}}$.
Задание: Заданы два графика описывающие процессы, проведенные в идеальном газе, которые переводят его из состояния А в состояние В и С (рис.1). В каком случае (АВ или АС) приращение внутренней энергии больше?
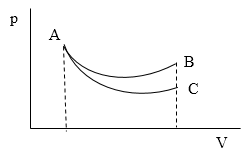
Рис. 1
Решение: Так как внутренняя энергия -- функция состояния, то ее изменение не зависит от хода процесса, рассмотрим только конечные состояния. Для процесса АВ запишем:
\[\triangle U_{AB}=\frac{i}{2}\nu R\left(T_B-T_A\right)\left(2.1\right)\]Из уравнения Менделеева - Клайперона:
\[p_AV_A-p_BV_B=\nu R\left(T_B-T_A\right)\to \triangle U_{AB}=\frac{i}{2}\left(p_BV_B-p_AV_A\right)\left(2.2\right)\]Для процесса АС запишем по аналогии:
\[\triangle U_{AС}=\frac{i}{2}\left(p_СV_С-p_AV_A\right)\left(2.3\right)\]Из рисунка 1 видно, что $V_B=V_С,\ а\ p_B>p_С$, следовательно, $\triangle U_{AB}>\triangle U_{AС}.$
Ответ: $\triangle U_{AB}>\triangle U_{AС}$.












