Ионная связь
Как известно, молекулы состоят из атомов. Электроны около ядра в атоме удерживаются кулоновскими силами притяжения разноимённых зарядов. Атом в целом, при этом электрически нейтрален. Силы, удерживающие вместе атомы в молекуле, по своей природе тоже электрические. Существует два типа связей атомов в молекуле: ионная связь и ковалентная. В некоторых атомах электрон (или электроны) очень слабо связаны с атомом в целом. Эти электроны легко теряются атомом, тогда образуется положительно заряженный ион. Либо все электроны очень крепко связаны с атомом, но при благоприятных условиях атом захватывает электрон или даже два и превращается в отрицательно заряженный ион. Между ионами существуют силы кулоновского притяжения, которые и обеспечивают образование молекулы. К числу таких молекул относят, например, молекулы N$a^+$C$l^-$. Потенциальная энергия притяжения ионов N$a^+$ и C$l^-$ равна:
где - заряд электрона, $r_0$- равновесное расстояние между ионами, ${\varepsilon }_0$- электрическая постоянная.
Наряду с энергией (1) существует энергия, связанная с силами отталкивания между ионами при их очень большом сближении, так как они не могут проникнуть друг в друга. Эти силы велики лишь при очень малых расстояниях между ионами и очень быстро убывают при увеличении этого расстояния. Соответственно, их вклад в полную энергию мал (около 10%). Поэтому для расчета энергии диссоциации ($\triangle E$) молекулы N$a^+$C$l^-$ используют соотношение: ($\triangle E=\left|U\right|$.
С физической точки зрения ионная связь характеризуется полным обменом зарядом (электроном) между ионами.
Ковалентная связь
При частичном обмене зарядом возникает ковалентная связь. Поясним, как образуется ковалентная связь:
Два положительных иона (например, в молекуле водорода $H_2$) отталкиваются кулоновскими силами. Поместим между ними посередине отрицательный заряд по модулю равный положительным зарядам ионов. Тогда со стороны этого заряда на положительные ионы действуют силы притяжения, в четыре раза большие, чем силы отталкивания положительных зарядов. Квантовая механика объясняет, как возникает движение электронов, при котором некоторые электроны при своем движении большую часть времени проводят между положительно заряженными ядрами.
Не существует универсального закона, описывающего межмолекулярное взаимодействие. Оно зависит от свойств молекул, условий взаимодействия, механизма его осуществления и других конкретных факторов. Межмолекулярное взаимодействие описывается всегда приближенными формулами с границами их справедливости.
Если средняя кинетическая энергия молекул меньше абсолютного значения средней энергии из взаимного притяжения (т.е., если энергия взаимодействия + кинетическая энергия отрицательна), то возникает связанное состояние системы молекул, т.е. либо жидкость, либо твердое тело.
Помимо сил, которые заставляют атомы образовывать молекулы, существуют и другие силы, которые заставляют взаимодействовать и молекулы. Они, например, являются причиной конденсации газов и превращения их в жидкие и твердые тела. Силы межмолекулярного взаимодействия, которые действуют в газах.
Три вида ван-дер-ваальсовских сил
Между молекулами любого газа действуют силы межмолекулярного притяжения и отталкивания. Они имеют электромагнитную и квантовую природу. Силы притяжения, которые проявляются на расстояниях между центрами молекул порядка $10^{-9}м$, называются ван-дер-ваальсовскими силами. Они являются причиной поправки на внутреннее давление в уравнении состояния Ван-дер Ваальса и убывают с расстоянием $\sim \frac{1}{r^7}$. Это соответствует потенциальной энергии, изменяющейся по закону:$U\sim \frac{1}{r^6}$.
Различают три вида ван-дер-ваальсовских сил:
- Ориентационные силы, действующие между двумя молекулами, которые обладают дипольными моментами pe и стремятся расположить молекулы упорядоченно так, чтобы векторы дипольных моментов ориентировались вдоль одной прямой. Этому препятствует тепловое движение молекул. При высоких температурах потенциальная энергия $U_{or}$ ориентационного взаимодействия равна: \[Uor=-\frac{p^4_e}{24{\pi }^2{\varepsilon }^2_0kT}\frac{1}{r^6}\left(2\right),\]
- Индукционные силы возникают между молекулами, обладающими высокой поляризуемостью. Если молекулы достаточно сближены, то под действием электрического поля одной из них в другой возникает индуцированный дипольный момент $\overrightarrow{p_e}={\varepsilon }_0\alpha \overrightarrow{E},\ $ где $\alpha $- поляризуемость молекулы, $\overrightarrow{E}$- напряженность поле первой молекулы. Потенциальная энергия Uind индукционного взаимодействия не зависит от температуры: \[U_{ind}=-\frac{\alpha p^2_e}{8{\pi }^2{\varepsilon }^2_0}\frac{1}{r^6}\left(3\right).\]
- Дисперсионные силы возникают в результате возбуждения колебаний электронов в молекуле (атоме) под влиянием колебаний электронов в других молекулах (атомах). Дисперсионное взаимодействие определяется нулевой энергией молекул (атомов), если колебания их могут быть рассмотрены как колебания линейных гармонических осцилляторов. В этом приближении потенциальная энергия $U_{disp}\ $дисперсиального взаимодействия: \[U_{disp}=-\frac{e^4{\nu }_0h}{32 \pi^2 {\varepsilon_o}^2 a^2}\frac{1}{r^6}\left(4\right),\]
где k - постоянная Больцмана, T - термодинамическая температура, ${\varepsilon }_0$- электрическая постоянная.
где $h$ - постоянная Планка, e -- элементарный заряд, ${\nu }_0=\frac{1}{2\pi }\sqrt{\frac{a}{m}}$, - частота колебаний атомов -- осцилляторов, a -- коэффициент пропорциональности.
Энергию дисперсного взаимодействия в первом приближении можно рассчитать при помощи формулы Лондона:
\[U_{disp}=-\left(\frac{1}{16{\pi }^2}\right)\left(\frac{3I_1I_2}{2\left(I_1{+I}_2\right)}\right)\left(\frac{{\alpha }_1{\alpha }_2}{r^6}\right)\left(2.3\right),\]где $I_1I_2$- потенциалы ионизации молекул. Они являются справочными для конкретных веществ.
Полная энергия ван-дер-ваальсовских сил:
\[U=U_{disp}+U_{ind}+Uor\ \left(5\right).\]Для полярных молекул основную роль играют ориентационные силы, для остальных -- дисперсионные. В большинстве случаев ван-дер -- ваальсовы силы притяжения перекрываются значительно превосходящими их химически валентными силами.
Межмолекулярное взаимодействие на малых расстояниях не может быть выражено степенным законом и носит сложный характер. Силы межмолекулярного взаимодействия определяют агрегатное состояние вещества.
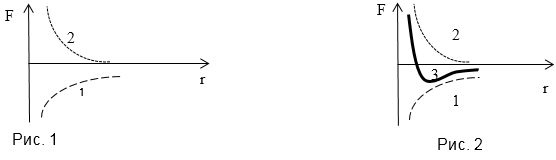
Задание: Силы отталкивания убывают с увеличением расстояния между центрами молекул по закону$f_{ott}\sim \frac{1}{r^n},\ где\ n\ge 13$ то есть значительно быстрее, чем силы притяжения. На рисунке (рис.1) представлены зависимость от r сил притяжения (1) и сил отталкивания кривая (2). Нарисуйте результирующую кривую взаимодействия.
Решение: Сложим, имеющиеся кривые графически, получим (3) кривая взаимодействия:
Задание: Для системы Kr-HCl (криптон -- хлороводород) укажите возможные виды межмолекулярных взаимодействий. Дипольные моменты веществ считать известными. Как рассчитать энергию разных видов взаимодействия при известных температуре (T) и расстоянии между диполями r?
Решение:
Криптон -- инертный газ, он имеет завершенную электронную оболочку, его собственный дипольный момент равен нулю. Он способен только к дисперсионному взаимодействию. Оно проявляется между атомами Kr-Kr.
Хлороводород -- соединение полярное, его электронная плотность смещена в сторону хлора. Полярные соединения способны ко всем видам взаимодействия между молекулами и между молекулами хлороводорода возникают ориентационные взаимодействия (HCl-HCl), но в паре с криптоном (HCl-Kr) ориентационные силы не проявляются -- возможен только индукционный и дисперсионный эффекты.
Средняя энергия ориентационного взаимодействия двух молекул с дипольными моментами${\ p}_{e1\ }и{\ p}_{e2\ }$ при температуре T:
\[U_1=-\frac{2}{3}\frac{p^2_{e1}p^2_{e2}}{{\left(4\pi {\varepsilon }_0\right)}^2}\frac{1}{r^6}\frac{1}{kT}\left(2.1\right),\]где r -- расстояние между диполями, k - постоянная Больцмана.
Величина энергии индуцированного взаимодействия зависит от величины постоянного дипольного момента ($p^2_{e1}$) полярной молекулы HCl и от поляризуемость криптона (${\alpha }_2$):
\[U_{ind}=-2\left(\frac{p^2_{e1}}{16{\pi }^2{\varepsilon }_0}\right)\left(\frac{{\alpha }_2}{r^6}\right)\left(2.2\right),\]где ${\alpha }_2=2,43\cdot 10^{-30}м^3$-- поляризуемость криптона (справочная величина).
Энергия дисперсного взаимодействия в первом приближении дает формула Лондона:
\[U_{disp}=-\left(\frac{1}{16{\pi }^2}\right)\left(\frac{3I_1I_2}{2\left(I_1{+I}_2\right)}\right)\left(\frac{{\alpha }_1б_2}{r^6}\right)\left(2.3\right),\]где $I_1I_2$- потенциалы ионизации молекул. Для криптона $I_1=4,1\cdot 10^2кДж/моль$, для HCl $I_2$=$12,3\cdot 10^2кДж/моль$ , зная r можно рассчитать энергию дисперсного взаимодействия.
Ответ: Общая энергия взаимодействия криптона и хлороводорода определяется как сумма U=$U_{disp}$+$U_{ind}+Uor$, где соответствующие энергии определены формулами (2.1), (2.2), (2.3).











